Question

正四面体的棱长为a，则相邻两个面的夹角的余弦是

1

3

．

Answer 1

分析：先确定相邻两个面的夹角，再利用余弦定理求解即可．

解答：解：如图，取BC中点E，则AE⊥BC，DE⊥BC

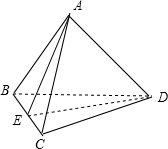
∴∠AED是相邻两个面的夹角
∵正四面体的棱长为a，
∴AE=DE=

3

2

a，AD=a，
∴cos∠AED=

3 4 a2+ 3 4 a2-a2

2× 3 2 a× 3 2 a

=

1

3

点评：本题考查面面角，考查余弦定理的运用，考查学生的计算能力，属于中档题．