题目内容
1.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且过点B(0,1).(Ⅰ)求椭圆的标准方程;
(Ⅱ)直线l:y=k(x+2)交椭圆于P、Q两点,若点B始终在以PQ为直径的圆内,求实数k的取值范围.
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}{b=1}\\{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解方程可求a,b进而可求方程;
(Ⅱ)设P(x1,y1),Q(x2,y2),联立$\left\{\begin{array}{l}{y=k(x=2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得:(1+4k2)x2+16k2x+(16k2-4)=0,由直线y=k(x+2)恒过点椭圆的左顶点(-2,0),可求x1,y1,由方程的根与系数关系可得,x1+x2,y1+y2,由已知可得,$\overrightarrow{BP}•\overrightarrow{BQ}<0$,根据向量的数量积的坐标表示可得关于k的不等式,求解即可.
解答 解:(Ⅰ)由题意知$\left\{\begin{array}{l}{b=1}\\{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\\{c=\sqrt{3}}\end{array}\right.$,
椭圆的标准方程为:$\frac{{x}^{2}}{4}+y=1$.…(4分)
(Ⅱ)设P(x1,y1),Q(x2,y2)
联立$\left\{\begin{array}{l}{y=k(x=2)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y,得:(1+4k2)x2+16k2x+(16k2-4)=0 …(6分)
依题意:直线l:y=k(x+2)恒过点(-2,0),此点为椭圆的左顶点,
所以x1=-2,y1=0,----①,
由方程的根与系数关系可得,x1+x2=$\frac{-16{k}^{2}}{1+4{k}^{2}}$-------②,
可得y1+y2=k(x1+2)+k(x2+2)=k(x1+x2)+4k----③,…(8分)
由①②③,${x}_{2}=\frac{2-8{k}^{2}}{1+4{k}^{2}}$,${y}_{2}=\frac{4k}{1+4{k}^{2}}$ …(10分)
由点B在以PQ为直径的圆内,得∠PBQ为钝角或平角,即$\overrightarrow{BP}•\overrightarrow{BQ}<0$.
$\overrightarrow{BP}$=(-2,-1),$\overrightarrow{BQ}$=(x2,y2-1)
∴$\overrightarrow{BP}•\overrightarrow{BQ}$=-2x2-y2+1<0.…(12分)
即$\frac{4-16{k}^{2}}{1+4{k}^{2}}+\frac{4k}{1+4{k}^{2}}-1>0$,整理可得,20k2-4k-3<0
解得:k$∈(-\frac{3}{10},\frac{1}{2})$.…(14分)
点评 本题主要考查了椭圆的性质在求解方程中的应用,直线与椭圆的位置关系的应用,试题对考试的逻辑思维能力及计算能力的要求较高.

| A. | 没有最大值,也没有最小值 | B. | 有最大值,没有最小值 | ||
| C. | 有最小值,没有最大值 | D. | 有最大值和最小值 |
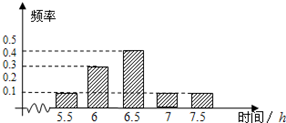 某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.
某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示. 某娱乐栏目有两名选手进行最后决赛,在赛前为调查甲、乙两位选手的受欢迎程度,随机地从现场选择了15位观众对两位选手进行评分,根据评分(评分越高表明越受观众欢迎),绘制茎叶图如下:
某娱乐栏目有两名选手进行最后决赛,在赛前为调查甲、乙两位选手的受欢迎程度,随机地从现场选择了15位观众对两位选手进行评分,根据评分(评分越高表明越受观众欢迎),绘制茎叶图如下: