题目内容
设f(x)=(ax+b)sinx+(cx+d)cosx,若已知f′(x)=xcosx,则f(x)=( )
| A.xsinx |
| B.xsinx-xcosx |
| C.xsinx+cosx |
| D.xcosx |
C
解析

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
若函数 在区间
在区间 上是单调函数,则实数
上是单调函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 在
在 处有极值,则
处有极值,则 的值为( ).
的值为( ).
A. | B. | C. | D. |
设曲线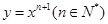 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为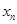 ,则
,则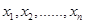 的乘积的值为( )
的乘积的值为( )
A.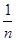 | B.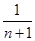 | C.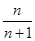 | D.1 |
函数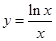 的最大值为( )
的最大值为( )
A.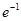 | B. | C.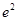 | D.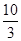 |
下列值等于1的定积分是( )
A. | B. | C. | D. |
设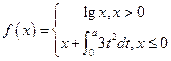 ,若f(f(1))=1,则a=( )
,若f(f(1))=1,则a=( )
| A.1 |
| B.2 |
| C.3 |
| D.4 |
若一球的半径为r,作内接于球的圆柱,则其圆柱侧面积最大为( )
| A.2πr2 |
| B.πr2 |
| C.4πr2 |
D.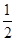 πr2 πr2 |
等差数列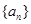 中的是函数
中的是函数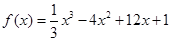 的极值点,则
的极值点,则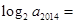
| A.2 | B.3 | C.4 | D.5 |