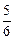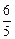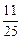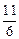题目内容
已知平面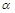 ∥
∥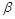 ,直线l
,直线l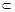
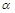 ,点P∈l,平面
,点P∈l,平面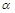 、
、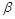 间的距离为5,则在
间的距离为5,则在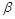 内到点P的距离为13且到直线l的距离为
内到点P的距离为13且到直线l的距离为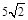 的点的轨迹是( )
的点的轨迹是( )
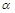 ∥
∥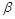 ,直线l
,直线l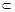
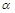 ,点P∈l,平面
,点P∈l,平面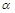 、
、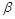 间的距离为5,则在
间的距离为5,则在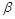 内到点P的距离为13且到直线l的距离为
内到点P的距离为13且到直线l的距离为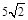 的点的轨迹是( )
的点的轨迹是( )| A.一个圆 | B.四个点 | C.两条直线 | D.双曲线的一支 |
B
专题:计算题.
分析:如图所示:作PH⊥β,H为垂足,过H 作直线m∥l,则m是l在平面β内的摄影.作HA⊥m,且HA=PH=5,则由三垂线定理可得 PA⊥l,作AM∥m,且 AM=
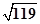 ,有勾股定理可得MP=13,故M在所求的轨迹上.据点M在面β内,可得满足条件的M共有4个.
,有勾股定理可得MP=13,故M在所求的轨迹上.据点M在面β内,可得满足条件的M共有4个.解答:
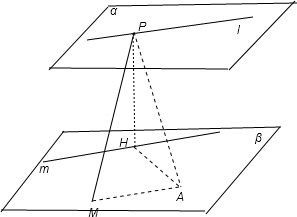 解:如图所示:作PH⊥β,H为垂足,则PH=5.
解:如图所示:作PH⊥β,H为垂足,则PH=5.过H 作直线m∥l,则m是l在平面β内的摄影.
作HA⊥m,且HA=PH=5,
则由三垂线定理可得 PA⊥m,∴PA⊥l,故 PA=5
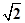 .
.作AM∥m,且 AM=
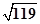 ,有勾股定理可得MP=13,故M在所求的轨迹上.又点M在面β内,
,有勾股定理可得MP=13,故M在所求的轨迹上.又点M在面β内,故满足条件的M共有4个,
故选 B.
点评:本题考查勾股定理、三垂线定理的应用,体现了数形结合的数学思想,确定点M的位置,是解题的难点和关键.

练习册系列答案
相关题目
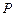 过点
过点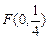 且与直线
且与直线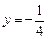 相切.
相切.
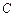 的方程;
的方程;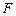 作一条直线交轨迹
作一条直线交轨迹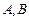 两点,轨迹
两点,轨迹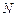 ,
,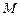 为线段
为线段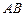 的中点,求证:
的中点,求证: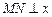 轴.
轴.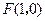 ,直线
,直线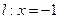 ,
,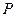 为平面上的动点,过点
为平面上的动点,过点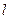 的垂线,垂足为点
的垂线,垂足为点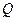 ,且
,且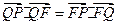 .
.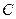 的方程;
的方程; 的直线交轨迹
的直线交轨迹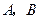 两
两 点,交直线
点,交直线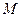 .
.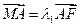 ,
,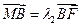 ,求
,求 的值;
的值;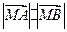 的最小值.
的最小值.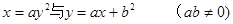 的图像只可能是下图中( *** )
的图像只可能是下图中( *** )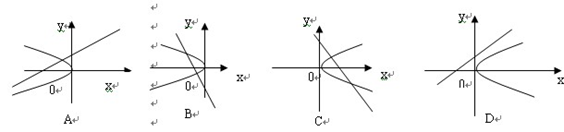
 ,点
,点 满足
满足 ,记点
,记点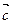 ="(1,1)" 的直线l与点P的轨迹交于A,B两点,当
="(1,1)" 的直线l与点P的轨迹交于A,B两点,当 时,求
时,求 AOB的面积。(9分)
AOB的面积。(9分) .
. 时,求
时,求 的最大、最小值.
的最大、最小值.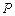 与点
与点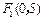 与点
与点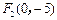 满足
满足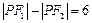 ,则点
,则点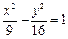
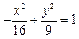
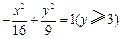
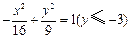

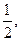 求点M的轨迹方程。
求点M的轨迹方程。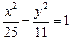 的左支上,
的左支上,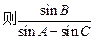 等于
等于