题目内容
已知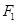 、
、 是椭圆
是椭圆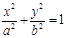
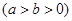 的左、右焦点,且离心率
的左、右焦点,且离心率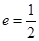 ,点
,点 为椭圆上的一个动点,
为椭圆上的一个动点,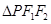 的内切圆面积的最大值为
的内切圆面积的最大值为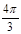 .
.
(1) 求椭圆的方程;
(2) 若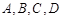 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量 与
与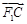 共线,
共线,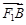 与
与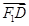 共
共
线,且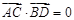 ,求
,求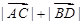 的取值范围.
的取值范围.
(1)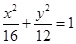 ;(2)
;(2) 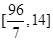
解析试题分析:本小题主要通过对直线与圆锥曲线中椭圆的综合应用的考查,具体涉及到椭圆方程的求法、直线与圆锥曲线的相关知识与圆锥曲线的综合知识,提示考生对圆锥曲线的综合题加以重视,本题主要考查考生的推理论证能力,运算求解能力、化归与转化以及数形结合的数学思想.(1)利用方程思想和几何性质,得到含有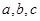 的两个等量关系,进而利用待定系数法求解椭圆方程;(2)通过直线与方程联立,借助韦达定理和弦长公式将
的两个等量关系,进而利用待定系数法求解椭圆方程;(2)通过直线与方程联立,借助韦达定理和弦长公式将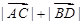 进行表示为含有
进行表示为含有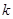 的函数关系式,利用换元法和二次函数求值域的思路寻求范围.
的函数关系式,利用换元法和二次函数求值域的思路寻求范围.
试题解析:(1)由几何性质可知:当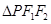 内切圆面积取最大值时,
内切圆面积取最大值时,
即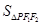 取最大值,且
取最大值,且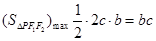 .
.
由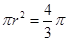 得
得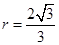
又 为定值,
为定值,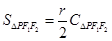 ,
,
综上得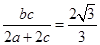 ;
;
又由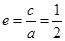 ,可得
,可得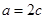 ,即
,即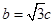 ,
,
经计算得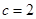 ,
,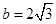 ,
,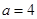 ,
,
故椭圆方程为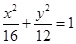 . (5分)
. (5分)
(2) ①当直线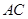 与
与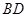 中有一条直线垂直于
中有一条直线垂直于 轴时,
轴时,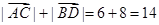 .
.
②当直线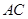 斜率存在但不为0时,设
斜率存在但不为0时,设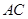 的方程为:
的方程为: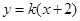 ,由
,由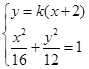 消去
消去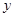
可得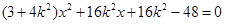 ,代入弦长公式得:
,代入弦长公式得: 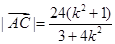 ,
,
同理由 消去
消去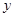 可得
可得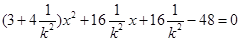 ,
,
代入弦长公式得: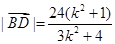 ,
,
所以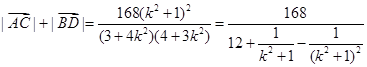
令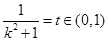 ,则
,则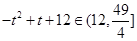 ,所以
,所以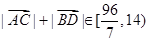 ,
,
由①②可知,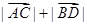 的取值范围是
的取值范围是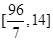 . (12分)
. (12分)
考点:(1)椭圆方程;(2)直线与椭圆的位置关系;(3)函数的值域.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
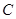 :
: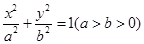 的离心率为
的离心率为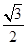 ,以椭圆
,以椭圆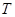 为圆心作圆
为圆心作圆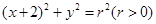 ,设圆
,设圆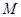 与点
与点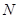 .
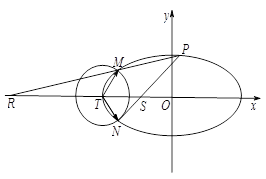
.
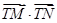 的最小值,并求此时圆
的最小值,并求此时圆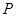 是椭圆
是椭圆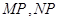 分别与
分别与 轴交于点
轴交于点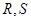 ,
,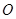 为坐标原点,
为坐标原点,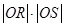 为定值.
为定值.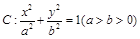 ,
, 为其右焦点,离心率为
为其右焦点,离心率为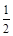 .
.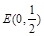 ,问是否存在直线
,问是否存在直线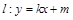 ,使
,使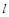 与椭圆
与椭圆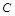 交于
交于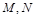 两点,且
两点,且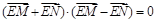 .若存在,求出
.若存在,求出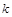 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.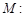
 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为 的菱形的四个顶点.
的菱形的四个顶点. 的方程;
的方程; 与椭圆
与椭圆 ,
,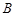 两点,且线段
两点,且线段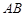 的垂直平分线经过点
的垂直平分线经过点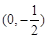 ,求
,求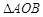 (
(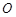 为原点)面积的最大值.
为原点)面积的最大值.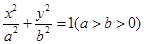 的右焦点为
的右焦点为 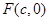 ,
,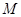 为椭圆的上顶点,
为椭圆的上顶点,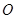 为坐标原点,且两焦点和短轴的两端构成边长为
为坐标原点,且两焦点和短轴的两端构成边长为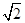 的正方形.
的正方形.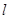 交与椭圆于
交与椭圆于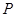 ,
, 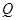 ,且使
,且使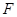 为
为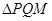 的垂心,若存在,求出
的垂心,若存在,求出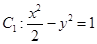 ,曲线
,曲线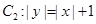 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.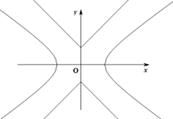
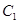 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);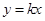 与
与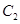 有公共点,求证
有公共点,求证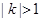 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;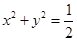 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.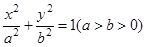 的离心率为
的离心率为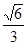 ,且过点
,且过点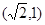 .
.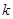 的直线
的直线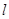 与椭圆相交于不同的两点
与椭圆相交于不同的两点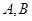 ,试问在
,试问在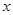 轴上是否存在点
轴上是否存在点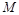 ,使
,使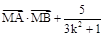 是与
是与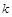 无关的常数?若存在,求出点
无关的常数?若存在,求出点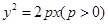 与椭圆
与椭圆 共焦点,
共焦点,
 的值和抛物线C的准线方程;
的值和抛物线C的准线方程;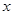 轴下方的一点,直线
轴下方的一点,直线 是抛物线C在点P处的切线,问是否存在平行于
是抛物线C在点P处的切线,问是否存在平行于 与抛物线C交于不同的两点A,B,且使
与抛物线C交于不同的两点A,B,且使 ?若存在,求出直线
?若存在,求出直线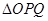 中,
中,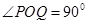 ,
,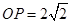 ,点
,点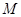 在线段
在线段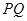 上.
上.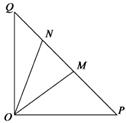
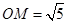 ,求
,求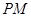 的长;
的长;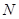 在线段
在线段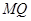 上,且
上,且 ,问:当
,问:当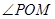 取何值时,
取何值时,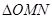 的面积最小?并求出面积的最小值.
的面积最小?并求出面积的最小值.