题目内容
设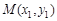 ,
,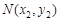 为不同的两点,直线
为不同的两点,直线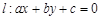 ,
,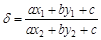 ,
,
以下命题中正确的序号为( ).
 不论
不论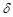 为何值,点N都不在直线
为何值,点N都不在直线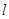 上;
上;
 若
若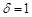 ,则过M,N的直线与直线
,则过M,N的直线与直线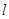 平行;
平行;
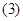 若
若 ,则直线
,则直线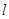 经过MN的中点;
经过MN的中点;
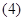 若
若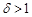 ,则点M、N在直线
,则点M、N在直线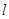 的同侧且直线
的同侧且直线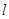 与线段MN的延长线相交.
与线段MN的延长线相交.
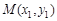 ,
,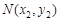 为不同的两点,直线
为不同的两点,直线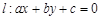 ,
,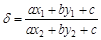 ,
,以下命题中正确的序号为( ).
 不论
不论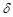 为何值,点N都不在直线
为何值,点N都不在直线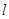 上;
上; 若
若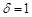 ,则过M,N的直线与直线
,则过M,N的直线与直线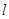 平行;
平行;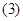 若
若 ,则直线
,则直线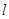 经过MN的中点;
经过MN的中点;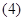 若
若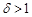 ,则点M、N在直线
,则点M、N在直线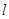 的同侧且直线
的同侧且直线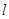 与线段MN的延长线相交.
与线段MN的延长线相交.| A.(1)(2)(3) | B.(2)(3)(4) | C.(1)(3)(4) | D.(1)(2)(3)(4) |
D
分析:
(1)根据δ中的分母不为0,即可判断点N不在直线l上;
(2)δ=1时,分b不等于0和等于0两种情况考虑,当b不为0时,根据δ=1,化简后得到直线MN的斜率与直线l的斜率相等,且点N不在直线l上,进而得到两直线平行;当b为0时,根据δ=1推出直线l与直线MN的斜率都不存在,进而得到两直线平行;
(3)当δ=-1时,化简后得到线段MN的中点满足直线l的解析式,进而得到MN的中点在直线l上;
(4)根据δ大于1,得到ax1+by1+c与ax2+by2+c同号且|ax1+by1+c|大于|ax2+by2+c|,进而得到点M、N在直线l的同侧且直线l与线段MN的延长线相交,综合可得答案。
解答:
(1)因为δ=
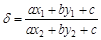 中,ax2+by2+c≠0,所以点N(x2,y2)不在直线l上,本选项正确;
中,ax2+by2+c≠0,所以点N(x2,y2)不在直线l上,本选项正确;(2)当b≠0时,根据δ=1,得到
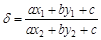 =1,化简得:y2-y1/ x2-x=-a/b,即直线MN的斜率为- a/b,
=1,化简得:y2-y1/ x2-x=-a/b,即直线MN的斜率为- a/b,又直线l的斜率为- a/b,由(1)知点N不在直线l上,得到直线MN与直线l平行;
当b=0时,根据δ=1,得到
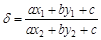 =1,
=1,化简得:x1=x2,直线MN与直线l的斜率不存在,都与y轴平行,
由(1)知点N不在直线l上,得到直线MN与直线l平行,
综上,当δ=1,直线MN与直线l平行,本选项正确;
(3)当δ=-1时,得到
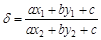 =-1,
=-1,化简得:a?(x1+x)/2+b?(y1+y2)/2+c=0,而线段MN的中点坐标为((x1+x)/2,(y1+y2)/2)。所以直线l经过MN的中点,本选项正确;
(4)当δ>1时,得到
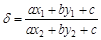 >1,
>1,即(ax1+by1+c)(ax2+by2+c)>0,所以点M、N在直线l的同侧,
且|ax1+by1+c|>|ax2+by2+c|,得到点M与点N到直线l的距离不等,所以延长线与直线l相交,本选项正确。
所以命题中正确的序号为:(1)、(2)、(3)、(4)。
点评:此题考查学生掌握一点是否在已知直线上的判别方法,掌握两直线平行时满足的条件,是一道中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

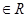 ,命题“
,命题“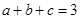 ,则
,则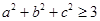 ”的否命题是( )
”的否命题是( )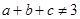 ,则
,则
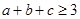 ,则
,则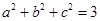
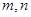 为两条不同的直线,
为两条不同的直线,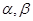 为两个不同的平面,下列四个命题真命题是
为两个不同的平面,下列四个命题真命题是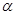 ∥
∥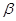 ,
,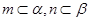 ,则
,则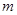 ∥
∥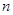
 ,且
,且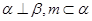 ,则
,则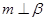
 则
则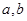 是异面直线,给出下列命题
是异面直线,给出下列命题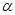 过直线
过直线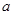 且与b平行.
且与b平行.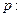 不等式
不等式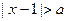 的解集为R;命题
的解集为R;命题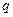 :
: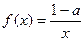 在区间
在区间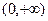 上是增函数.若命题“
上是增函数.若命题“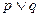 ”为假命题,求实数
”为假命题,求实数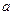 的取值范围.
的取值范围.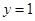 是幂函数;
是幂函数;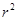 来刻画回归效果,
来刻画回归效果,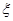 服从正态分布N(0,1),若
服从正态分布N(0,1),若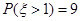 ,则
,则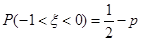 ;
;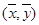
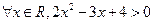 ;
;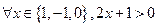 ;③
;③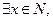 使
使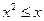 ;
;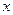 为
为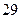 的约数。则所有正确命题的序号有
的约数。则所有正确命题的序号有 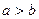 ,则
,则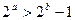 ”的否命题为______
”的否命题为______ 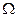 ,如果连接
,如果连接