题目内容
解答题
(理)已知f(x)＝ln(ex＋a)(a＞0)(1)求y＝f(x)的反函数及f(x)的导函数．(2)假设x∈[ln3a，ln4a]，不等式：|m－f－1(x)|＋lnf′(x)＜0恒成立求m范围．
答案：
解析：
解析：
|
解：先求f′(x)＝ 原不等式等价于ln(ex－a)－ln(ex＋a)＋x＜m＜ln(ex－a)＋ln(ex＋a)－x(5分) 设f1(x)＝ln(ex－a)－ln(ex＋a)＋x f2(x)＝ln(ex－a)＋ln(ex＋a)－x 又f′2(x)＝ ∴f1(x)的最大值＝f1(ln4a)＝ln f2(x)的最小值＝f2(ln3a)＝ln ∴ln |
(2分)再求f－1(x)＝ln(ex－a)(x＞lna)(4分)
－1＞0
a(8分)
a(11分)
a＜m＜ln
a(12分)
练习册系列答案
相关题目
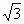sin2x＋a(a∈R)
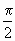]时，f(x)的最大值为4，求a的值．
＞0．
相邻两项an，an+1是方程
的两根(n∈N+)且a1＝2，Sn＝c1＋c2＋…＋cn，求an与S2n．
，f(x)是一个递增等差数列{an}的前3项
．
时，记h(A)＝f(A，B)，试求h(A)的表达式及定义域；
的图象？若存在，求出向量p的坐标；若不存在，请说明