题目内容
如图，△ABC是边长为a的正三角形，现随机向圆所在区域投一点，则该点恰好落在△ABC内的概率是（ ）分析：根据正三角形的性质算出外接圆半径等于
a，从而得到外接圆的面积S=
．再由三角形面积公式算出△ABC的面积S'=
，根据几何概型公式加以计算，可得所求概率．
| ||
| 3 |
| πa2 |
| 3 |
| ||
| 4 |
解答：解：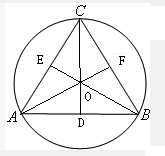
设O为外接圆的圆心，则O是三条高线CD、BE、AF的交点，
可得CO=
CD=
×
a=
a，
∴△ABC的外接圆面积为S=π×(
a)2=
又∵△ABC的面积为S'=
×a×a×sin60°=
，
∴随机向圆所在区域投一点，
则该点恰好落在△ABC内的概率P=
=
=
．
故选：B
设O为外接圆的圆心，则O是三条高线CD、BE、AF的交点，可得CO=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
∴△ABC的外接圆面积为S=π×(
| ||
| 3 |
| πa2 |
| 3 |
又∵△ABC的面积为S'=
| 1 |
| 2 |
| ||
| 4 |
∴随机向圆所在区域投一点，
则该点恰好落在△ABC内的概率P=
| S′ |
| S |
| ||||
|
3
| ||
| 4π |
故选：B
点评：本题给出几何概型，求点恰好落在△ABC内的概率．着重考查了正三角形的性质、三角形与圆的面积计算和几何概型的计算等知识，属于中档题．
练习册系列答案
相关题目
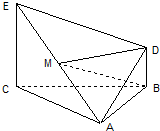如图：△ABC是边长为2的正三角形，EC⊥面ABC，BD∥CE，且CE=CA=2BD，M是EA的中点．
（2012•徐州模拟）如图，△ABC是边长为
（2012•江苏三模）如图，△ABC是边长为
（2013•普陀区二模）如图，△ABC是边长为1的正三角形，点P在△ABC所在的平面内，且