题目内容
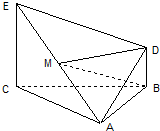 如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.
如图:△ABC是边长为2的正三角形,EC⊥面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.①求证:DE=DA;
②求证:DM∥面ABC;
③求C到面ADE的距离.
分析:①利用勾股定理求得DE和AD 的长,从而得到结论.
②设AC的中点为F,证得BDMF为矩形,可得BF∥DM,进而证得DM∥平面ABC.
③易证DM⊥平面AEC,故平面ADE⊥平面AEC,过C作CH⊥AE,则CH⊥平面ADE,面积法求得CH的值.
②设AC的中点为F,证得BDMF为矩形,可得BF∥DM,进而证得DM∥平面ABC.
③易证DM⊥平面AEC,故平面ADE⊥平面AEC,过C作CH⊥AE,则CH⊥平面ADE,面积法求得CH的值.
解答:解:①证明:∵EC⊥面ABC,BD∥CE,∴DB⊥平面ABC.∵△ABC是边长为2的正三角形且CE=CA=2BD,
∴在直角三角形ABC中,可求得AD=
. 在直角梯形ECBD中,可求得DE=
,∴DE=AD.
②证明:设AC的中点为F,则MF∥EC,MF=
EC,由①DB∥EC,DB=
EC,
∴MF∥DB,MF=DB,故BDMF为矩形,∴BF∥DM. 又∵DM?平面ABC,BF?平面ABC,∴DM∥平面ABC.
③易证DM⊥平面AEC,∴平面ADE⊥平面AEC,
过C作CH⊥AE,则CH⊥平面ADE,故CH之长为点C到平面ADE的距离,
由面积法求得 CH=
=
.
∴在直角三角形ABC中,可求得AD=
| 5 |
| 5 |
②证明:设AC的中点为F,则MF∥EC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴MF∥DB,MF=DB,故BDMF为矩形,∴BF∥DM. 又∵DM?平面ABC,BF?平面ABC,∴DM∥平面ABC.
③易证DM⊥平面AEC,∴平面ADE⊥平面AEC,
过C作CH⊥AE,则CH⊥平面ADE,故CH之长为点C到平面ADE的距离,
由面积法求得 CH=
| CA•CE |
| AE |
| 2 |
点评:本题考查证明线段相等,线面平行的方法,构造矩形BDMF是解题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 如图,△ABC是边长为a的正三角形,现随机向圆所在区域投一点,则该点恰好落在△ABC内的概率是( )
如图,△ABC是边长为a的正三角形,现随机向圆所在区域投一点,则该点恰好落在△ABC内的概率是( ) (2012•徐州模拟)如图,△ABC是边长为
(2012•徐州模拟)如图,△ABC是边长为 (2012•江苏三模)如图,△ABC是边长为
(2012•江苏三模)如图,△ABC是边长为 (2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且
(2013•普陀区二模)如图,△ABC是边长为1的正三角形,点P在△ABC所在的平面内,且