题目内容
设函数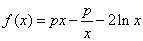 ,
,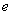 是自然对数的底数.
是自然对数的底数.
(Ⅰ)若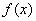 在其定义域内为单调函数,求
在其定义域内为单调函数,求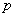 的取值范围;
的取值范围;
(Ⅱ)设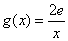 ,若在
,若在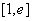 上至少存在一点
上至少存在一点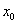 ,使得
,使得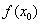 >
>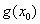 成立,求实数
成立,求实数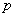 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)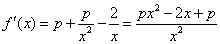 ——2分
——2分
令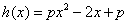 ,要使
,要使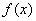 在其定义域
在其定义域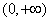 内是单调函数,只需
内是单调函数,只需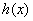 在定义域
在定义域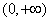 内满足
内满足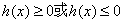 恒成立.
恒成立.
①若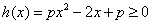 恒成立,则
恒成立,则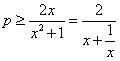 在
在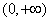 上恒成立
上恒成立
∴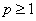
②若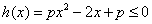 恒成立,则
恒成立,则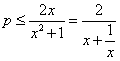 在
在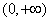 上恒成立
上恒成立
∴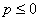
综上所述,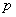 的取值范围为
的取值范围为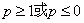 .
——6分
.
——6分
(Ⅱ)当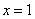 时,不等式显然不成立,
时,不等式显然不成立,
当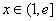 时,由
时,由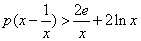 得
得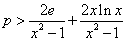 ,
,
令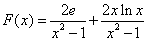
由题意,若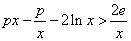 在
在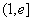 上有解,则
上有解,则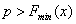
由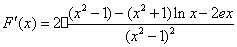
令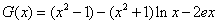 ,
,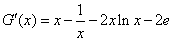
∵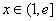 ∴
∴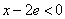 ,
,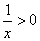 ,
,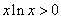 ∴
∴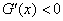
∴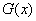 在
在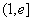 上单调递减 ∴
上单调递减 ∴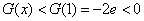 , 即
, 即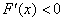 ∴
∴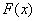 在
在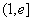 上单调递减 ∴
上单调递减 ∴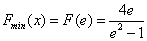
∴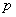 的取值范围是
的取值范围是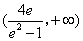 .
——12分
.
——12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,其中
,其中 且
且 .
.
 ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由. ,
, ,其中
,其中 且
且 .
.
 ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数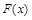 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由. ,
, ,其中
,其中 且
且 .
. ,求函数
,求函数 的单调递增区间;
的单调递增区间; 时,函数
时,函数 有极值,求函数
有极值,求函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.