题目内容
下列命题:
①当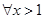 时,
时,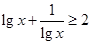 ;
;
②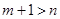 是
是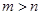 成立的充分不必要条件;
成立的充分不必要条件;
③对于任意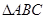 的内角
的内角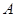 、
、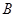 、
、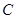 满足:
满足: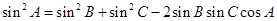 ;
;
④定义:如果对任意一个三角形,只要它的三边长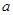 、
、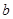 、
、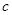 都在函数
都在函数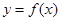 的定义域内,就有
的定义域内,就有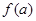 、
、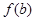 、
、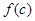 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称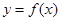 为“三角形型函数”.函数
为“三角形型函数”.函数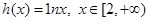 是“三角形型函数”.
是“三角形型函数”.
其中正确命题的序号为 .(填上所有正确命题的序号)
①当
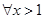 时,
时,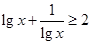 ;
;②
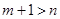 是
是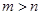 成立的充分不必要条件;
成立的充分不必要条件;③对于任意
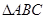 的内角
的内角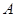 、
、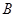 、
、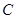 满足:
满足: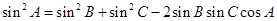 ;
;④定义:如果对任意一个三角形,只要它的三边长
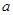 、
、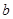 、
、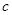 都在函数
都在函数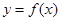 的定义域内,就有
的定义域内,就有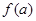 、
、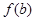 、
、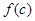 也是某个三角形的三边长,则称
也是某个三角形的三边长,则称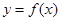 为“三角形型函数”.函数
为“三角形型函数”.函数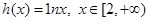 是“三角形型函数”.
是“三角形型函数”.其中正确命题的序号为 .(填上所有正确命题的序号)
①③④
试题分析:由基本不等式,①正确,又
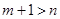 不能推出
不能推出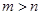 ,所以②错,由余弦定理
,所以②错,由余弦定理 , 再由正弦定理边角互化得,
, 再由正弦定理边角互化得,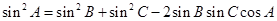 ,所以③正确.
,所以③正确.对任意一个三角形三边长
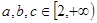 ,且
,且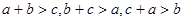 ,
,则
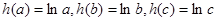 ,因为
,因为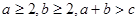 ,所以
,所以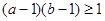 ,所以
,所以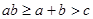 ,所以
,所以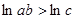 ,即
,即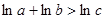 .
.同理可证明
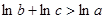 l,
l,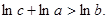
所以
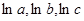 是一个三角形的三边长.
是一个三角形的三边长.故函数
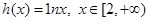 ,是三角形型函数.④正确.
,是三角形型函数.④正确.点评本题为新定义题,正确理解定义是解题的关键,考查综合分析和解决问题的能力.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
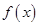 在[a,b]上为单调函数”是“函数
在[a,b]上为单调函数”是“函数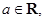 则“
则“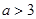 ”是“
”是“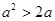 ”的 条件. (填“充要”、“充分不必要”、“必要不充分”或“既不充分也不必要”)
”的 条件. (填“充要”、“充分不必要”、“必要不充分”或“既不充分也不必要”)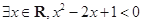 ”的否定是: .
”的否定是: . 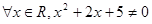 ”的否定是____________.
”的否定是____________.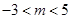 ”是“方程
”是“方程 表示双曲线”的( )
表示双曲线”的( ) 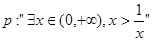 ,命题p的否定为命题q,则q的真假性为 .(填真或假).
,命题p的否定为命题q,则q的真假性为 .(填真或假).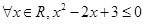 ”的否定是( )
”的否定是( )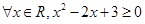
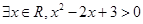
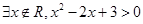
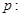 函数
函数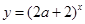 是增函数.命题
是增函数.命题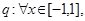
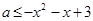 成立,若
成立,若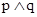 为真命题,求实数
为真命题,求实数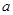 的取值范围.
的取值范围.