题目内容
(Ⅰ)在如图的坐标系中作出同时满足约束条件:x+y-1≥0;x-y+1≥0;4x+y-2≥0的可行性区域;(Ⅱ)若实数x,y满足(Ⅰ)中约束条件,求目标函数
| x+y | x |
分析:(Ⅰ)先画出直线x+y-1=0;x-y+1=0,4x+y-2=0,然后根据不等式画出是直线的上方区域还是下方区域,从而得到可行域;
(II)根据目标函数
的几何意义,而
表示区域里的点与坐标原点连线的斜率,只需求出
的范围即可求出目标函数
的取值范围.
(II)根据目标函数
| x+y |
| x |
| y |
| x |
| y |
| x |
| x+y |
| x |
解答:解:(Ⅰ)
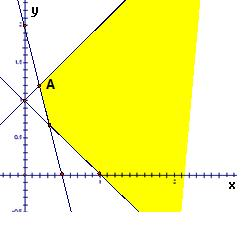
(Ⅱ)点A(
,
),令t=
∈(-1,6]则
=1+t∈(0,7]

(Ⅱ)点A(
| 1 |
| 5 |
| 6 |
| 5 |
| y |
| x |
| x+y |
| x |
点评:本题主要考查了简单的线性规划,正确理解不等式所表示的区域,以及目标函数的几何意义,属于基础题.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)= 已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=2-x.
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=2-x.
 是定义在R上的偶函数,当
是定义在R上的偶函数,当 时,
时, .
.
 时,
时,