题目内容
(12分)已知数列{an},{bn}是各项均为正数的等比数列,设cn= (n∈N*).
(n∈N*).
(1)数列{cn}是否为等比数列?证明你的结论;
(2)设数列|ln an|,|1n bn|的前n项和分别为Sn,Tn. 若a1="2," . 求数列{cn}的前n项和.
. 求数列{cn}的前n项和.
 (n∈N*).
(n∈N*).(1)数列{cn}是否为等比数列?证明你的结论;
(2)设数列|ln an|,|1n bn|的前n项和分别为Sn,Tn. 若a1="2,"
 . 求数列{cn}的前n项和.
. 求数列{cn}的前n项和.(1)略
(2)4+42+…+4n=
 (4n-1)
(4n-1)(1){cn}是等比数列.(2分)
证明:设{an}的公比为q1(q1>0),{bn}的公比为q2(q2>0),则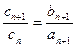 ·
· ·
· ≠0,故{cn}为等比数列.(5分)
≠0,故{cn}为等比数列.(5分)
(2)数列{1n an}和{1n bn}分别是公差为1n q1和1n q2的等差数列. 由条件得 =
= ,即
,即 .(7分)
.(7分)
故对n=1,2,…,(2lnq1-1nq2)n2+(4lna1-1nq1-2lnb1+1nq2)n+(2lna1-1nq1)=0.
于是
将a1=2代入得q1="4," q2="16," b1=8.(10分)
从而有cn= ="4n." 所以数列{cn}的前n项和为4+42+…+4n=
="4n." 所以数列{cn}的前n项和为4+42+…+4n= (4n-1).(12分)
(4n-1).(12分)
证明:设{an}的公比为q1(q1>0),{bn}的公比为q2(q2>0),则
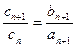 ·
· ·
· ≠0,故{cn}为等比数列.(5分)
≠0,故{cn}为等比数列.(5分)(2)数列{1n an}和{1n bn}分别是公差为1n q1和1n q2的等差数列. 由条件得
 =
= ,即
,即 .(7分)
.(7分)故对n=1,2,…,(2lnq1-1nq2)n2+(4lna1-1nq1-2lnb1+1nq2)n+(2lna1-1nq1)=0.
于是

将a1=2代入得q1="4," q2="16," b1=8.(10分)
从而有cn=
 ="4n." 所以数列{cn}的前n项和为4+42+…+4n=
="4n." 所以数列{cn}的前n项和为4+42+…+4n= (4n-1).(12分)
(4n-1).(12分)
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 是以
是以 为首项,
为首项, 为公比的等比数列.令
为公比的等比数列.令 ,
, ,
, .
. 和
和 ;
; ,
, 且
且 ,试比较
,试比较 的大小;
的大小; ,其中
,其中 成等比数列.若存在,求出实数对
成等比数列.若存在,求出实数对 列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。 n=
n= ,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。
,sn=b1+b2+┉+bn,对任意正整数n,sn+(n+m)an+1<0恒成立,试求m的取值范围。 为等比数列,
为等比数列, ,
, 则
则 ( )
( ) 
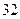

 中,
中, ,
, ,则前9项之和等于 .
,则前9项之和等于 . 的前n项和是
的前n项和是 ,若
,若
 在等比数列
在等比数列 中,若
中,若 ,
, ,则
,则 ▲ .
▲ .  中,
中, ,
, 和
和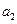 的等比中项等于
的等比中项等于 ,则
,则 ( )
( )

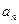 }的前n 项和为
}的前n 项和为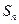 ,若
,若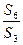 ="3" ,则
="3" ,则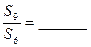 .
.