题目内容
已知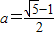 ,函数f(x)=logax,若正实数m,n满足f(m)>f(n),则m,n的大小关系为 .
,函数f(x)=logax,若正实数m,n满足f(m)>f(n),则m,n的大小关系为 .
【答案】分析:因为已知条件中对数函数的底数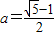 ,即0<a<1,故函数f(x)=logax在(0,+∞)上为减函数,根据函数的单调性,结合足f(m)>f(n),不难判断出m,n的大小关系.
,即0<a<1,故函数f(x)=logax在(0,+∞)上为减函数,根据函数的单调性,结合足f(m)>f(n),不难判断出m,n的大小关系.
解答:解:∵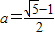
∴0<a<1
∴f(x)=logax在(0,+∞)上为减函数
若f(m)>f(n)
则m<n
故答案为:m<n
点评:函数y=ax和函数y=logax,在底数a>1时,指数函数和对数函数在其定义域上均为增函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为减函数,而f(-x)与f(x)的图象关于Y轴对称,其单调性相反,故函数y=a-x和函数y=loga(-x),在底数a>1时,指数函数和对数函数在其定义域上均为减函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为增函数.
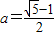 ,即0<a<1,故函数f(x)=logax在(0,+∞)上为减函数,根据函数的单调性,结合足f(m)>f(n),不难判断出m,n的大小关系.
,即0<a<1,故函数f(x)=logax在(0,+∞)上为减函数,根据函数的单调性,结合足f(m)>f(n),不难判断出m,n的大小关系.解答:解:∵
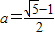
∴0<a<1
∴f(x)=logax在(0,+∞)上为减函数
若f(m)>f(n)
则m<n
故答案为:m<n
点评:函数y=ax和函数y=logax,在底数a>1时,指数函数和对数函数在其定义域上均为增函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为减函数,而f(-x)与f(x)的图象关于Y轴对称,其单调性相反,故函数y=a-x和函数y=loga(-x),在底数a>1时,指数函数和对数函数在其定义域上均为减函数,当底数0<a<1时,指数函数和对数函数在其定义域上均为增函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目