题目内容
已知椭圆C1的方程为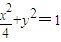 ,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.(1)求双曲线C2的方程;
(2)若直线
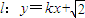 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且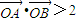 (其中O为原点),求k的范围.
(其中O为原点),求k的范围.(3)试根据轨迹C2和直线l,设计一个与x轴上某点有关的三角形形状问题,并予以解答(本题将根据所设计的问题思维层次评分).
【答案】分析:(1)设双曲线C2的方程为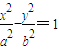 ,则a2=4-1=3,再由a2+b2=c2得b2=1,由此能求出故C2的方程.
,则a2=4-1=3,再由a2+b2=c2得b2=1,由此能求出故C2的方程.
(2)将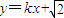 代入
代入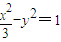 得
得 .由直线l与双曲线C2交于不同的两点得:
.由直线l与双曲线C2交于不同的两点得: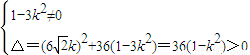 ,由此能求出k的取值范围.
,由此能求出k的取值范围.
(3)若x轴上存在点P(m,0),使△APB是以AB为底边的等腰三角形,求m的取值范围.
当k=0时,P点坐标为(0,0),即m=0;当k≠0时,设线段AB的中点M(x,y),线段AB的中垂线方程为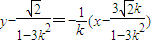 ,令y=0,得
,令y=0,得 ,由此能求出m的范围.
,由此能求出m的范围.
解答:解:(1)设双曲线C2的方程为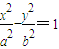 ,
,
则a2=4-1=3,再由a2+b2=c2得b2=1,故C2的方程为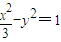
(2)将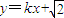 代入
代入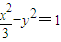 得
得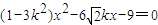
由直线l与双曲线C2交于不同的两点得: ∴
∴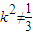 且k2<1…①A(x1,y1),B(x2,y2),则
且k2<1…①A(x1,y1),B(x2,y2),则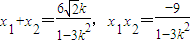 ∴
∴ =
=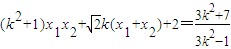
又∵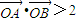 ,得x1x2+y1y2>2,∴
,得x1x2+y1y2>2,∴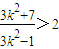
即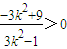 ,解得:
,解得: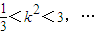 ②,故k的取值范围为
②,故k的取值范围为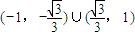 .
.
(3)若x轴上存在点P(m,0),使△APB是以AB为底边的等腰三角形,求m的取值范围.
解:显然,当k=0时,P点坐标为(0,0),即m=0;
当k≠0时,设线段AB的中点M(x,y),
由(2)知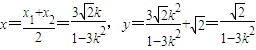
于是,线段AB的中垂线方程为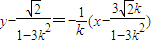 ,令y=0,得
,令y=0,得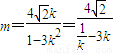 ,由①知,
,由①知,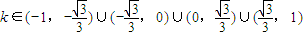
∴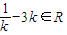 ,∴m∈R,且m≠0.
,∴m∈R,且m≠0.
综上所述,m∈R.
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
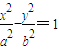 ,则a2=4-1=3,再由a2+b2=c2得b2=1,由此能求出故C2的方程.
,则a2=4-1=3,再由a2+b2=c2得b2=1,由此能求出故C2的方程.(2)将
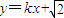 代入
代入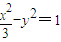 得
得 .由直线l与双曲线C2交于不同的两点得:
.由直线l与双曲线C2交于不同的两点得: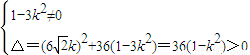 ,由此能求出k的取值范围.
,由此能求出k的取值范围.(3)若x轴上存在点P(m,0),使△APB是以AB为底边的等腰三角形,求m的取值范围.
当k=0时,P点坐标为(0,0),即m=0;当k≠0时,设线段AB的中点M(x,y),线段AB的中垂线方程为
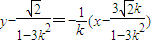 ,令y=0,得
,令y=0,得 ,由此能求出m的范围.
,由此能求出m的范围.解答:解:(1)设双曲线C2的方程为
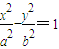 ,
,则a2=4-1=3,再由a2+b2=c2得b2=1,故C2的方程为
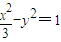
(2)将
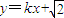 代入
代入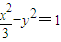 得
得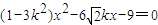
由直线l与双曲线C2交于不同的两点得:
 ∴
∴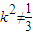 且k2<1…①A(x1,y1),B(x2,y2),则
且k2<1…①A(x1,y1),B(x2,y2),则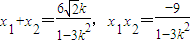 ∴
∴ =
=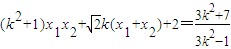
又∵
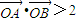 ,得x1x2+y1y2>2,∴
,得x1x2+y1y2>2,∴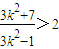
即
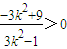 ,解得:
,解得: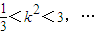 ②,故k的取值范围为
②,故k的取值范围为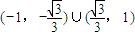 .
.(3)若x轴上存在点P(m,0),使△APB是以AB为底边的等腰三角形,求m的取值范围.
解:显然,当k=0时,P点坐标为(0,0),即m=0;
当k≠0时,设线段AB的中点M(x,y),
由(2)知
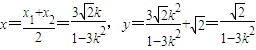
于是,线段AB的中垂线方程为
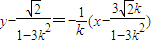 ,令y=0,得
,令y=0,得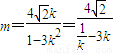 ,由①知,
,由①知,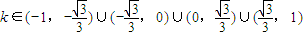
∴
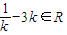 ,∴m∈R,且m≠0.
,∴m∈R,且m≠0.综上所述,m∈R.
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目