题目内容
在算式“4×□+1×△=30”的□,△中,分别填入一个正整数,使它们的倒数之和最小,则这两个数构成的数对(□,△)应为________.
(5,10)
分析:设这两个正整数分别为m、n,则4m+n=30,再利用“1”的代换,利用基本不等式,即可求得结论.
解答:设这两个正整数分别为m、n,则4m+n=30,
∴ =
=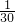 ×(
×( )(4m+n)=
)(4m+n)=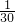 (5+
(5+ +
+ )≥
)≥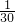 (5+4)=
(5+4)=
当且仅当 =
= 即n=2m,∴6m=30,∴m=5,n=10时取等号
即n=2m,∴6m=30,∴m=5,n=10时取等号
∴当m=5,n=10时, 取得最小值
取得最小值
∴□处为5,△处为10
故答案为(5,10)
点评:本题考查合情推理,考查基本不等式的运用,正确运用基本不等式是关键.
分析:设这两个正整数分别为m、n,则4m+n=30,再利用“1”的代换,利用基本不等式,即可求得结论.
解答:设这两个正整数分别为m、n,则4m+n=30,
∴
 =
=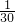 ×(
×( )(4m+n)=
)(4m+n)=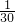 (5+
(5+ +
+ )≥
)≥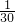 (5+4)=
(5+4)=
当且仅当
 =
= 即n=2m,∴6m=30,∴m=5,n=10时取等号
即n=2m,∴6m=30,∴m=5,n=10时取等号∴当m=5,n=10时,
 取得最小值
取得最小值
∴□处为5,△处为10
故答案为(5,10)
点评:本题考查合情推理,考查基本不等式的运用,正确运用基本不等式是关键.

练习册系列答案
相关题目
在算式“
+
=
”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为( )
| 4 |
| △ |
| 1 |
| Θ |
| 30 |
| △×Θ |
| A、6,6 | B、10,5 |
| C、14,4 | D、18,3 |