题目内容
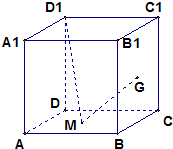 已知正方体的棱长ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,M为面ABCD上一点,则D1M+GM的最小值为
已知正方体的棱长ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,M为面ABCD上一点,则D1M+GM的最小值为分析:建立空间直角坐标系,利用对称性以及两点间的距离公式求出D1M+GM的最小值.
解答:解:建立空间直角坐标系如图,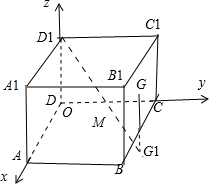 ;
;
∵正方体ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,
∴G(1,2,1),作G关于平面xoy的对称点G1,则G1(1,2,-1),又D1(0,0,2),
∴D1M+MG=D1M+MG1=D1G1=
=
,
∴D1M+GM的最小值为
;
故答案为:
.
 ;
;∵正方体ABCD-A1B1C1D1的棱长为2,G是面BB1C1C的中心,
∴G(1,2,1),作G关于平面xoy的对称点G1,则G1(1,2,-1),又D1(0,0,2),
∴D1M+MG=D1M+MG1=D1G1=
| (1-0)2+(2-0)2+(-1-2)2 |
| 14 |
∴D1M+GM的最小值为
| 14 |
故答案为:
| 14 |
点评:本题以正方体为载体考查了利用对称性求最小值的问题,是基础题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
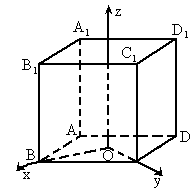
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( ) 的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标. 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;
 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
 的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
的棱长为2,分别按下列要求建立空间直角坐标系,请写出正方体各顶点的坐标.
 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系;

 的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
的指向为Ox轴、Oy轴、Oz轴的正方向,建立直角坐标系.
 的棱长为2,
的棱长为2, 分别是
分别是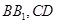 的中点.
的中点. 的体积;
的体积;