题目内容
15.如图,在四面体ABCD中,E、F分别是棱AD、BC的中点,则向量$\overrightarrow{EF}$与$\overrightarrow{AB}$、$\overrightarrow{CD}$的关系是( )
| A. | $\overrightarrow{EF}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{CD}$ | B. | $\overrightarrow{EF}=-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{CD}$ | C. | $\overrightarrow{EF}=\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{CD}$ | D. | $\overrightarrow{EF}=-\frac{1}{2}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{CD}$ |
分析 根据向量的三角形法则,以及向量的加减几何意义即可求出.
解答 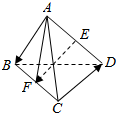 解:连接AF,$\overrightarrow{EF}$=$\overrightarrow{AF}$-$\overrightarrow{AE}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)-$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$($\overrightarrow{AD}$-$\overrightarrow{AC}$)=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{CD}$,
解:连接AF,$\overrightarrow{EF}$=$\overrightarrow{AF}$-$\overrightarrow{AE}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)-$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$($\overrightarrow{AD}$-$\overrightarrow{AC}$)=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{CD}$,
故选:C.
点评 本题考查了向量的三角形法则,以及向量的几何意义,属于基础题.

练习册系列答案
相关题目
7.已知f(x)是定义在R上的奇函数,对任意x∈R恒有f(x-2)=f(x)+f(2),且当x∈(0,1)时,f(x)=2x-1,则f(log236)=( )
| A. | 35 | B. | $-\frac{7}{16}$ | C. | $-\frac{7}{9}$ | D. | $\frac{7}{16}$ |