题目内容
若函数f（x）同时满足：①对于定义域上的任意x，恒有f（-x）+f（x）=0；②对于定义域上的任意x1，x2，当x1≠x2时，恒有
，则称函数f（x）为“理想函数”，给出下列四个函数中：①f（x）=2x
②f（x）=-
③f（x）=
④f（x）=
⑤f（x）=
能被称为“理想函数”的有 ．
【答案】分析：根据已知中“理想函数”中条件①等价于函数为奇函数；条件②等价于函数在R上为增函数；逐一判断五个函数的单调性和奇偶性，可得答案．
解答：解：若条件①成立，则函数为奇函数；若条件②成立，则函数在R上为增函数；
①中函数f（x）=2x即是奇函数，又在R上为增函数，故①是“理想函数”；
②中函数f（x）=-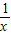
是奇函数，但在R上不是增函数，故②不是“理想函数”；
③中函数f（x）=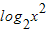
是偶函数，且在R上不是增函数，故③不是“理想函数”；
④中函数f（x）=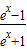
是奇函数，又在R上为增函数，故④是“理想函数”；
⑤中函数f（x）=
是奇函数，又在R上为增函数，故⑤是“理想函数”；
故五个函数中①④⑤为“理想函数”；
故答案为：①④⑤
点评：本题以命题的真假判断为载体考查了函数的奇偶性和单调性，熟练掌握各种初等基本函数单调性和奇偶性是解答的关键．
解答：解：若条件①成立，则函数为奇函数；若条件②成立，则函数在R上为增函数；
①中函数f（x）=2x即是奇函数，又在R上为增函数，故①是“理想函数”；
②中函数f（x）=-
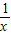是奇函数，但在R上不是增函数，故②不是“理想函数”；③中函数f（x）=
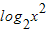是偶函数，且在R上不是增函数，故③不是“理想函数”；④中函数f（x）=
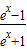是奇函数，又在R上为增函数，故④是“理想函数”；⑤中函数f（x）=
是奇函数，又在R上为增函数，故⑤是“理想函数”；故五个函数中①④⑤为“理想函数”；
故答案为：①④⑤
点评：本题以命题的真假判断为载体考查了函数的奇偶性和单调性，熟练掌握各种初等基本函数单调性和奇偶性是解答的关键．
练习册系列答案
相关题目
若函数f（x）同时满足①有反函数；②是奇函数；③定义域与值域相同．则f（x）的解析式可能是（ ）
| A、f（x）=-x3 | ||
| B、f（x）=x3+1 | ||
C、f（x）=
| ||
D、f（x）=lg
|
若函数f（x）同时满足下列三个性质：
①最小正周期为π；
②图象关于直线x=
对称；
③在区间[-
，
]上是增函数．
则y=f（x）的解析式可以是（ ）
①最小正周期为π；
②图象关于直线x=
| π |
| 3 |
③在区间[-
| π |
| 6 |
| π |
| 3 |
则y=f（x）的解析式可以是（ ）
A、y=sin（2x-
| ||||
B、y=sin（
| ||||
C、y=cos（2x-
| ||||
D、y=cos（2x+
|