题目内容
若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0; ②对于定义域上的任意x1,x2,当x1≠x2时,恒有
<0,则称函数f(x)为“理想函数”.给出下列四个函数中:
(1)f(x)=
(2)f(x)=x2
(3)f(x)=
(4)f(x)=
,
能被称为“理想函数”的有
| f(x1)-f(x2) |
| x1-x2 |
(1)f(x)=
| 1 |
| x |
(2)f(x)=x2
(3)f(x)=
| 2x-1 |
| 2x+1 |
(4)f(x)=
|
能被称为“理想函数”的有
(4)
(4)
(填相应的序号).分析:先理解已知两条性质反映的函数性质,①f(x)为奇函数,②f(x)为定义域上的单调减函数,由此意义判断题干所给四个函数是否同时具备两个性质即可
解答:解:依题意,性质①反映函数f(x)为定义域上的奇函数,性质②反映函数f(x)为定义域上的单调减函数,
(1)f(x)=
为定义域上的奇函数,但不是定义域上的单调减函数,其单调区间为(-∞,0),(0,+∞),故排除(1);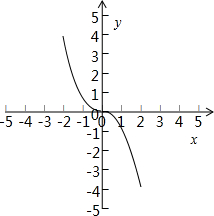
(2)f(x)=x2 为定义域上的偶函数,排除(2);
(3)f(x)=
=1-
,定义域为R,由于y=2x+1在R上为增函数,故函数f(x)为R上的增函数,排除(3);
(4)f(x)=
的图象如图:显然此函数为奇函数,且在定义域上为减函数,故(4)为理想函数
故答案为 (4)
(1)f(x)=
| 1 |
| x |
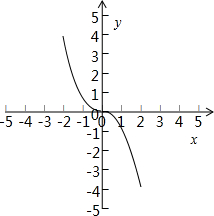
(2)f(x)=x2 为定义域上的偶函数,排除(2);
(3)f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
(4)f(x)=
|
故答案为 (4)
点评:本题主要考查了抽象表达式反映的函数性质,对新定义函数的理解能力,奇函数的定义,函数单调性的定义,基本初等函数的单调性和奇偶性及其判断方法,复合函数及分段函数的单调性和奇偶性的判断方法

练习册系列答案
相关题目
若函数f(x)同时满足①有反函数;②是奇函数;③定义域与值域相同.则f(x)的解析式可能是( )
| A、f(x)=-x3 | ||
| B、f(x)=x3+1 | ||
C、f(x)=
| ||
D、f(x)=lg
|
若函数f(x)同时满足下列三个性质:
①最小正周期为π;
②图象关于直线x=
对称;
③在区间[-
,
]上是增函数.
则y=f(x)的解析式可以是( )
①最小正周期为π;
②图象关于直线x=
| π |
| 3 |
③在区间[-
| π |
| 6 |
| π |
| 3 |
则y=f(x)的解析式可以是( )
A、y=sin(2x-
| ||||
B、y=sin(
| ||||
C、y=cos(2x-
| ||||
D、y=cos(2x+
|