Question

【题目】选修4—1：几何证明选讲

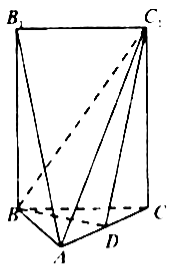
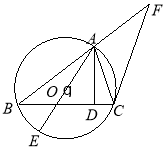
如图，已知圆是的外接圆, ,是边上的高,是圆的直径，过点作圆的切线交的延长线于点.

（Ⅰ）求证：；

（Ⅱ）若，求的长.

Answer 1

【答案】（1）详见解析；（2）

【解析】

试题分析：（I）如图所示，连接BE．由于AE是⊙O的直径，可得∠ABE=90°．利用∠E与∠ACB都是弧AB所对的圆周角，可得∠E=∠ACB．进而得到△ABE∽△ADC，即可得到．（II）利用切割线定理可得，可得BF．再利用△AFC∽△CFB，可得，进而根据sin∠ACD=sin∠AEB，，即可得出答案．

试题解析: （Ⅰ）证明：连结，由题意知为直角三角形

因为，，

所以

即

又，所以

（Ⅱ）因为是圆的切线，所以，

又，所以，

因为，所以

所以，得,

所以