题目内容
(08年上虞市质量调测一理)如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=![]() ,M为BC的中点,
,M为BC的中点,
(Ⅰ) 证明:AM⊥PM;
(Ⅱ)求二面角P―AM―D的大小;
(III)求点D到平面AMP的距离.
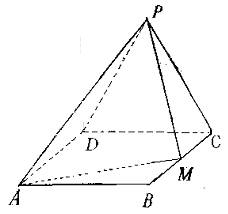
解析:解法1:(I)取CD的中点E,连结PE、EM、EA
∵△PCD为正三角形 ∴PE⊥CD,PE=PDsin∠PDE=2sin60°=![]()
∵平面PCD⊥平面ABCD ∴PE⊥平面ABCD
∵四边形ABCD是矩形 ∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得EM=![]() ,AM=
,AM=![]() ,AE=3 ∴EM2+AM2=AE2
,AE=3 ∴EM2+AM2=AE2
∴∠AME=90° ∴AM⊥PM
(Ⅱ)由(I)可知EM⊥AM,PM⊥AM ∴∠PME是二面角P―AM―D的平面角
∴tan∠PME=![]() ∴∠PMA=45° ∴二面角P―AM―D为45°
∴∠PMA=45° ∴二面角P―AM―D为45°
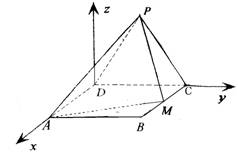
解法2:(I)以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系D―xyz,
依题意,可得D(0,0,0),P(0,1,![]() ),C(0,2,0),A(2
),C(0,2,0),A(2![]() ,0,0),
,0,0),
M(![]() ,2,0),
,2,0),![]()
![]()
![]()
即![]() ,∴AM⊥PM.
,∴AM⊥PM.
(Ⅱ)设![]() 平面PAM,则
平面PAM,则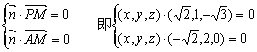
![]()
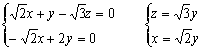
取y=1,得![]() 显然
显然![]() 平面ABCD
平面ABCD
![]() .
.
结合图形可知,二面角P―AM―D为45°;

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案