题目内容
在等差数列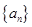 和等比数列
和等比数列 中,a1=2b1=2,b6=32,
中,a1=2b1=2,b6=32,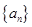 的前20项
的前20项
和S20=230.
(Ⅰ)求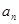 和
和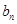 ;
;
(Ⅱ)现分别从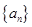 和
和 的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
的前4中各随机抽取一项,写出相应的基本事件,并求所取两项中,满足an>bn的概率.
【答案】
(Ⅰ) an=n+1 (Ⅱ) bn=2n-1
【解析】本事主要是考查了等差数列和等比数列的通项公式以及古典概型的概率的求解的综合运用。
(1)因为a1=2b1=2,b6=32, S20=230.借助于通项公式和前n项和的公式得到结论。
(2)首先分析所有的基本事件数,然后分析事件发生的基本事件数,进而结合古典概型求解概率的值。
解:(1)设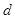 是数列
是数列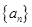 的公差,
的公差, 是
是 的公比,由题意得:
的公比,由题意得:
an=n+1, ……3分
bn=2n-1 ……7分
(2)分别从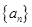 ,
, 中的前三项中各随机抽取一项,得到基本事件(2,1), (2,2), (2,4), (2,8), (3,1),
(3,2), (3,4), (3,8), (4,1), (4,2), (4,4) (4,8), (5,1), (5,2) (5,4), (5,8),有16个, ……12分
中的前三项中各随机抽取一项,得到基本事件(2,1), (2,2), (2,4), (2,8), (3,1),
(3,2), (3,4), (3,8), (4,1), (4,2), (4,4) (4,8), (5,1), (5,2) (5,4), (5,8),有16个, ……12分
符合条件的有8个,故所求概率为0.5. ……14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 和等比数列
和等比数列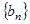 中,
中,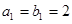 ,
, ,
, 是
是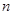 项和.
项和.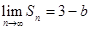 ,求实数
,求实数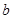 的值;
的值; 中?若存在,求出所有的
中?若存在,求出所有的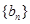 中至少有三项在数列
中至少有三项在数列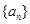 中,但
中,但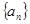 和等比数列
和等比数列 中,
中,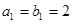 ,
,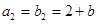 ,
, 是
是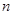 项和.
项和.
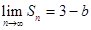 ,求实数
,求实数 的值;
的值;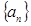 中?若存在,求出所有的
中?若存在,求出所有的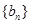 中至少有三项在数列
中至少有三项在数列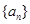 中,但
中,但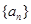 和等比数列
和等比数列 中,
中, ,
,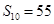 .
.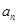 和
和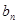 ;
;