题目内容
函数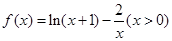 的零点所在的区间是( )
的零点所在的区间是( )
A.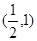 | B.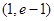 | C.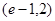 | D.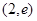 |
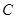
解析试题分析:令函数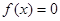 ,则有
,则有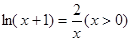 ,设函数
,设函数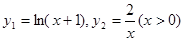 ,此时零点即两个函数的交点.因为函数
,此时零点即两个函数的交点.因为函数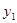 过点
过点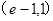 ,且
,且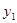 在
在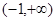 上递增,所以当
上递增,所以当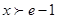 时,
时,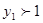 ;函数
;函数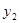 过点
过点 ,且函数
,且函数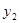 在
在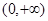 上递减.所以当
上递减.所以当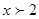 时,
时,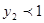 ,所以两者的交点只有一个,在区间
,所以两者的交点只有一个,在区间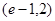 .
.
考点:函数零点的判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数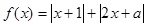 的最小值为3,则实数
的最小值为3,则实数 的值为( )
的值为( )
| A.5或8 | B.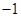 或5 或5 | C.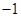 或 或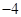 | D.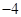 或8 或8 |
设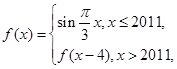 则f(2 016)=( )
则f(2 016)=( )
A.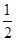 | B.-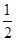 | C.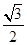 | D.-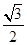 |
(5分)(2011•陕西)方程|x|=cosx在(﹣∞,+∞)内( )
| A.没有根 | B.有且仅有一个根 | C.有且仅有两个根 | D.有无穷多个根 |
下图揭示了一个由区间 到实数集
到实数集 上的对应过程:区间
上的对应过程:区间 内的任意实数
内的任意实数 与数轴上的线段
与数轴上的线段 (不包括端点)上的点
(不包括端点)上的点 一一对应(图一),将线段
一一对应(图一),将线段 围成一个圆,使两端
围成一个圆,使两端 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线 与
与 轴交于点
轴交于点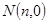 ,由此得到一个函数
,由此得到一个函数 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( )
 ;
;  是偶函数;
是偶函数;  在其定义域上是增函数;
在其定义域上是增函数;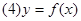 的图像关于点
的图像关于点 对称.
对称.
| A.(1)(3)(4). | B.(1)(2)(3). | C.(1)(2)(4). | D.(1)(2)(3)(4). |
已知函数f(x)的定义域为[3,6],则函数y= 的定义域为( )
的定义域为( )
A.[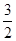 ,+∞) ,+∞) | B.[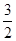 ,2) ,2) |
C.(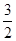 ,+∞) ,+∞) | D.[ ,2) ,2) |
若函数f(x)=x2-2x,g(x)=ax+2(a>0),?x1∈[-1,2],?x0∈[-1,2],使g(x1)=f(x0),则a的取值范围是( )
A.(0,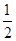 ] ] | B.[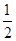 ,3] ,3] | C.[3,+∞) | D.(0,3] |
下列函数中,不满足f(2x)=2f(x)的是( )
| A.f(x)=|x| | B.f(x)=x-|x| |
| C.f(x)=x+1 | D.f(x)=-x |