题目内容
(本题满分10分)
已知函数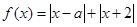 (a为常数,且a∈R).
(a为常数,且a∈R).
(1)若函数f (x)的最小值为2,求a的值;
(2)当a=2时,解不等式f (x)≤6.
(1)a=0或a=-4(2)
解析试题分析:(Ⅰ)f (x)=|x-a|+|x+2|=| a-x |+|x+2|
≥|a-x+x+2|=|a+2|,
由|a+2|=2,解得a=0或a=-4. ……5分(Ⅱ)f (x)= |x-2|+|x+2|.
当x<-2时,不等式为2-x-x-2≤6,其解为-3≤x<-2;
当-2≤x<2时,不等式为2-x+x+2≤6恒成立,其解为-2≤x<2;
当x≥2时,不等式为x-2+x+2≤6,其解为2≤x≤3;
所以不等式f (x)≤6的解集为[-3,3]. ……10分
如有其它解法,相应给分.
考点:本小题主要考查绝对值不等式的性质和绝对值不等式的解法,考查学生的运算求解能力.
点评:含绝对值的不等式越来越成为高考的考点和热点问题,要准确掌握,灵活应用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
已知等比数列 ,
,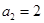 ,则其前三项和
,则其前三项和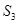 的取值范围是( )
的取值范围是( )
A.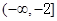 | B.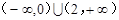 |
C.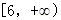 | D.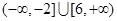 |
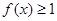 在区间(-∞,+∞)上恒成立,求实数a的取值范围
在区间(-∞,+∞)上恒成立,求实数a的取值范围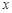 的不等式
的不等式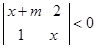 的解集为
的解集为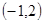 。
。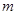 的值;
的值;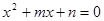 的一个根
的一个根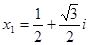 ,求
,求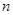 .
.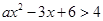 的解集为
的解集为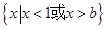 .
.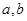 ;
;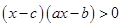 .
.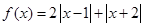 (1)求不等式
(1)求不等式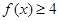 的解集;
的解集;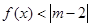 的解集是非空集合,求实数m的取值范围.
的解集是非空集合,求实数m的取值范围.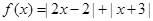 .
.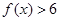 ;
; 的不等式
的不等式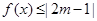 的解集不是空集,试求实数
的解集不是空集,试求实数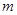 的取值范围.
的取值范围. 的不等式
的不等式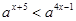 (
(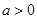 ,且
,且 ).
).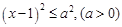 的解集为A,函数
的解集为A,函数 的定义域为B.
的定义域为B.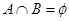 ,求
,求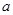 的取值范围;
的取值范围; 的图象关于原点对称。
的图象关于原点对称。