题目内容
附加题:A.如图,四边形ABCD内接于圆O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
求证:AB2=BE•CD.
B.设数列{an},{bn}满足an+1=3an+2bn,bn+1=2bn,且满足
 =M
=M ,试求二阶矩阵M.
,试求二阶矩阵M.C.已知椭圆C的极坐标方程为
 ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和.D.已知x,y,z均为正数.求证:
 .
.
【答案】分析:A:连接AC,因为EA切圆O于A,所以∠EAB=∠ACB.因为弧AB=弧AD,所以AB=AD,∠EAB=∠ACD,又四边形ABCD内接于圆O,所以△ABE∽CDA.所以AB2=BE•CD.
B:由题设得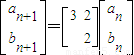 ,设
,设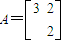 ,则M=A4.由矩阵的运算法则能够求出二阶矩阵M的值.
,则M=A4.由矩阵的运算法则能够求出二阶矩阵M的值.
C:直线l普通方程为y=x-2;曲线C的普通方程为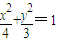 .由此能够求出点F1,F2到直线l的距离之和.
.由此能够求出点F1,F2到直线l的距离之和.
D:因为x,y,z都是为正数.所以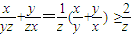 ,同理可得
,同理可得 ,
,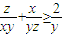 ,由此可得
,由此可得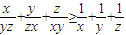 .
.
解答:A.证:连接AC,因为EA切圆O于A,所以∠EAB=∠ACB.
因为弧AB=弧AD,所以∠ACD=∠ACB,AB=AD,于是∠EAB=∠ACD(5分)
又四边形ABCD内接于圆O,所以∠ABE=∠D,所以△ABE∽CDA.
于是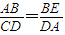 ,即AB•DA=BE•CD,所以AB2=BE•CD(10分)
,即AB•DA=BE•CD,所以AB2=BE•CD(10分)
B解:由题设得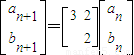 ,设
,设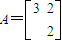 ,则M=A4.(5分)
,则M=A4.(5分)
 M=A4=(A2)2=
M=A4=(A2)2=
 =
=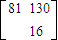 .(10分)
.(10分)
C解:(1)直线l普通方程为y=x-2;
曲线C的普通方程为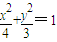 .(5分)
.(5分)
∵F1(-1,0),F2(1,0),
∴点F1到直线l的距离d1=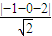 =
=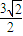 点F2到直线l的距离d2=
点F2到直线l的距离d2=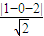 =
=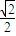 ,
,
∴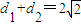 .(10分)
.(10分)
D证明:因为x,y,z都是为正数.所以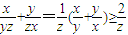 ,
,
同理可得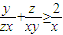 ,
,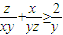 ,当且仅当x=y=z时,以上三式等号都成立.
,当且仅当x=y=z时,以上三式等号都成立.
将上述三个不等式两边分别相加,并除以2,得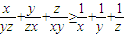 .(10分)
.(10分)
点评:本题考查二阶矩阵、极坐标方程、直线的参数方程和不等式的证明,解题时要认真审题,注意公式的合理运用.
B:由题设得
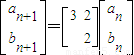 ,设
,设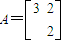 ,则M=A4.由矩阵的运算法则能够求出二阶矩阵M的值.
,则M=A4.由矩阵的运算法则能够求出二阶矩阵M的值.C:直线l普通方程为y=x-2;曲线C的普通方程为
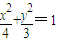 .由此能够求出点F1,F2到直线l的距离之和.
.由此能够求出点F1,F2到直线l的距离之和.D:因为x,y,z都是为正数.所以
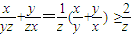 ,同理可得
,同理可得 ,
,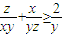 ,由此可得
,由此可得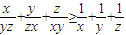 .
.解答:A.证:连接AC,因为EA切圆O于A,所以∠EAB=∠ACB.
因为弧AB=弧AD,所以∠ACD=∠ACB,AB=AD,于是∠EAB=∠ACD(5分)
又四边形ABCD内接于圆O,所以∠ABE=∠D,所以△ABE∽CDA.
于是
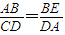 ,即AB•DA=BE•CD,所以AB2=BE•CD(10分)
,即AB•DA=BE•CD,所以AB2=BE•CD(10分)B解:由题设得
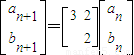 ,设
,设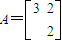 ,则M=A4.(5分)
,则M=A4.(5分) M=A4=(A2)2=
M=A4=(A2)2=
 =
=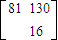 .(10分)
.(10分)C解:(1)直线l普通方程为y=x-2;
曲线C的普通方程为
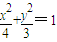 .(5分)
.(5分)∵F1(-1,0),F2(1,0),
∴点F1到直线l的距离d1=
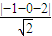 =
=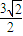 点F2到直线l的距离d2=
点F2到直线l的距离d2=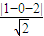 =
=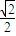 ,
,∴
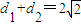 .(10分)
.(10分)D证明:因为x,y,z都是为正数.所以
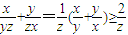 ,
,同理可得
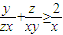 ,
,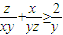 ,当且仅当x=y=z时,以上三式等号都成立.
,当且仅当x=y=z时,以上三式等号都成立.将上述三个不等式两边分别相加,并除以2,得
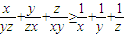 .(10分)
.(10分)点评:本题考查二阶矩阵、极坐标方程、直线的参数方程和不等式的证明,解题时要认真审题,注意公式的合理运用.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题) ,求线段AC的长度.
,求线段AC的长度. 和特征值λ2=2及对应的一个特征向量
和特征值λ2=2及对应的一个特征向量 ,试求矩阵A.
,试求矩阵A. (θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(θ是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
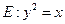
 与圆
与圆 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。