题目内容
函数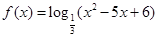 的单调递增区间为 .
的单调递增区间为 .
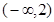
解析试题分析:由函数定义域得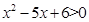 ,解得
,解得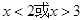 ,令
,令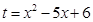 ,则
,则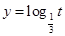 ,由这两个函数的图象,结合复合函数“同增异减”的规律,不难得出函数的增区间为
,由这两个函数的图象,结合复合函数“同增异减”的规律,不难得出函数的增区间为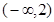 .
.
考点:复合函数的单调性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
函数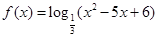 的单调递增区间为 .
的单调递增区间为 .
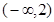
解析试题分析:由函数定义域得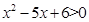 ,解得
,解得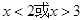 ,令
,令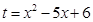 ,则
,则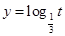 ,由这两个函数的图象,结合复合函数“同增异减”的规律,不难得出函数的增区间为
,由这两个函数的图象,结合复合函数“同增异减”的规律,不难得出函数的增区间为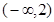 .
.
考点:复合函数的单调性

 阅读快车系列答案
阅读快车系列答案