题目内容
选修4—2:矩阵与变换
二阶矩阵M有特征值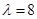 ,其对应的一个特征向量e=
,其对应的一个特征向量e=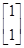 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点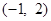
变换成点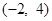 ,求矩阵M.
,求矩阵M.
二阶矩阵M有特征值
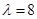 ,其对应的一个特征向量e=
,其对应的一个特征向量e=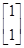 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点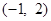
变换成点
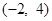 ,求矩阵M.
,求矩阵M.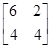
设M=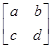 ,则由
,则由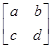
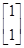 =8
=8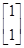 得
得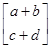 =
=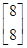 ,即a+b=c+d=8. 2分
,即a+b=c+d=8. 2分
由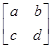
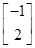 =
=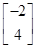 ,得
,得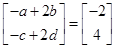 ,从而-a+2b=-2,-c+2d=4. 5分
,从而-a+2b=-2,-c+2d=4. 5分
由a+b =8及-a+2b=-2,解得a=6,b=2;
由c+d =8及-c+2d=4,解得c=4,b="4." 所以M=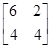 . 10分
. 10分
【命题意图】本题考查矩阵特征值及特征向量、矩阵的乘法等知识 ,意在考查运算求解能力.
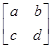 ,则由
,则由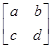
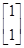 =8
=8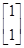 得
得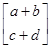 =
=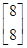 ,即a+b=c+d=8. 2分
,即a+b=c+d=8. 2分由
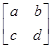
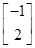 =
=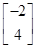 ,得
,得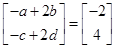 ,从而-a+2b=-2,-c+2d=4. 5分
,从而-a+2b=-2,-c+2d=4. 5分由a+b =8及-a+2b=-2,解得a=6,b=2;
由c+d =8及-c+2d=4,解得c=4,b="4." 所以M=
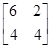 . 10分
. 10分【命题意图】本题考查矩阵特征值及特征向量、矩阵的乘法等知识 ,意在考查运算求解能力.

练习册系列答案
相关题目
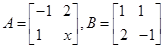 ,向量
,向量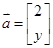 ,
,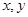 是实数,若
是实数,若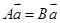 ,求
,求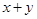 的值.
的值.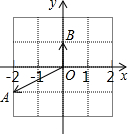
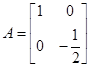 ,则矩阵A的逆矩阵为
,则矩阵A的逆矩阵为  ;(2)M=
;(2)M= .
. +
+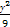 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.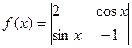 的值域是 .
的值域是 .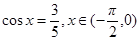 ,则
,则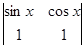 =_______
=_______