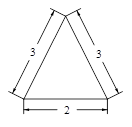
题目内容
如图,四棱锥P-ABCD中,AD∥BC,∠ADC=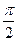 ,
,
PC⊥平面ABCD,点E为AB中点。AC⊥DE,
其中AD=1,PC=2,CD=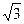 ;
;
(1)求异面直线DE与PB所成角的余弦值;
(2)求直线PC与平面PDE所成角的余弦值。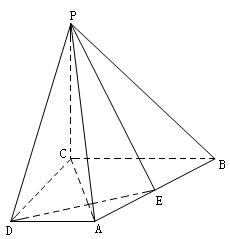
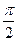 ,
,PC⊥平面ABCD,点E为AB中点。AC⊥DE,
其中AD=1,PC=2,CD=
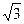 ;
;(1)求异面直线DE与PB所成角的余弦值;
(2)求直线PC与平面PDE所成角的余弦值。


解:(1)如图建立空间坐标系
设BC=
 ,则A(1,
,则A(1,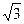 ,0),D(0,
,0),D(0,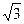 ,0)
,0)B(
 ,0,0),E(
,0,0),E( ,
, ,0),
,0), (0,0,2)
(0,0,2) (1,
(1,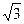 ,0),
,0), (
( ,
, ,
,
∵AC⊥DE
∴


∴E(
 ,
, ,0)
,0)所以


所以直线DE与PB所成角的余弦值为
 ;
;(2)设平面PDE的一个法向量
 (
( ,
, ,
, )
) ,
,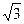 ,-2),
,-2), (
( ,
, ,
,
 ,
,

令
 ,得
,得 ,
,
所以
 (
( ,
, ,
, )
)设直线PC与平面PDE所成的角为

∵
 (0,0,2)
(0,0,2)∴
 ,
, =
=

∴
 .
.略

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直,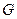 是
是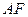 的中点.
的中点.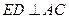 ;
;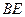 与平面
与平面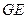 与
与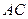 所成角的余弦值.
所成角的余弦值.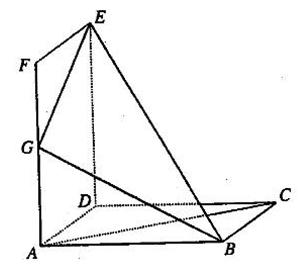
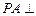 平面
平面 ,
,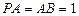 ,
,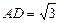 ,
, 是
是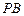 中点,点
中点,点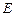 在
在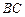 边上.
边上.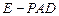 的体积;
的体积;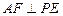 ;
;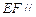 平面
平面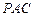 ,试确定
,试确定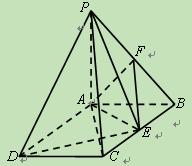
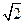 ,E、F分别是AB、CD的中点,EF=
,E、F分别是AB、CD的中点,EF=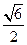 求异面直线AD和BC所成的角。
求异面直线AD和BC所成的角。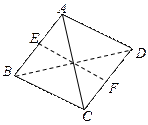
 B
B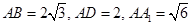 ,则点
,则点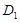 到直线AC的距离是
到直线AC的距离是 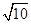
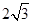
 a
a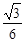 a
a a
a a
a
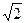 ,BC=CC1=1,P是BC1上一动点,则
,BC=CC1=1,P是BC1上一动点,则 的最小值是_____.
的最小值是_____.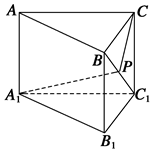
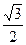


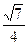
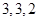 的三角形,则该圆锥的侧面积是 。
的三角形,则该圆锥的侧面积是 。