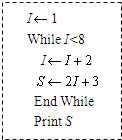题目内容

已知函数f（x）=
2x-1，x≥0
x2，x＜0
，则f（f（-2））=
 
．
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（-2）=（-2）2=4，从而能求出f（f（-2））=24-1=15．
解答： 解：∵f（x）=
2x-1，x≥0
x2，x＜0
，
∴f（-2）=（-2）2=4，
f（f（-2））=24-1=15．
故答案为：15．
点评：本题考查函数值的求法，是基础题，解题时要注意分段函数的性质的合理运用．
练习册系列答案
相关题目
抛物线x2=-
2
3
y的焦点的纵坐标与它的通径的比是（　　）
A、4
B、-4
C、
1
4
D、-
1
4
定义运算a*b为：a*b=
a(a≤b)
b(a＞b)
，如1*2=1，则函数f（x）=2x*2-x的值域为
 
．
在进位制转换中，412（5）=
 
（7）．
根据如图所示的伪代码，可知输出的结果S为
 
．
已知A={（x，y）|y=x2}，B={(x，y)|y=
x
}，则A∩B=（　　）
A、R
B、[0，+∞）
C、（1，1）
D、{（0，0），（1，1）}
函数y=sin（
x-π
2
）sinx的最小正周期是
 
．
y=3sin2x的最大值为
 
．
若集合A={0，1，2，3，4}，集合B={x|x∈A且x-2∉A}，则集合B的子集的个数为 （　　）
A、1B、2C、4D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网