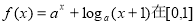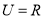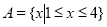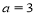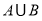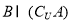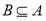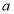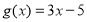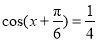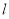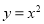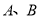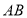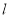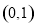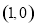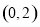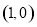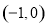题目内容
已知函数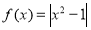 ,
,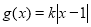 .
.
(Ⅰ)已知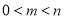 ,若
,若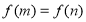 ,求
,求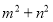 的值;
的值;
(Ⅱ)设 ,当
,当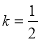 时,求
时,求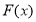 在
在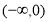 上的最小值;
上的最小值;
(Ⅲ)求函数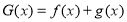 在区间
在区间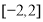 上的最大值.
上的最大值.
(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当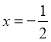 时,
时,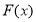 最小值为
最小值为 ;(Ⅲ)当
;(Ⅲ)当 时,
时, 在
在 上的最大值为0;当
上的最大值为0;当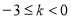 时,
时, 在
在 上的最大值为
上的最大值为 ;当
;当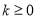 时,
时, 在
在 上的最大值为
上的最大值为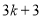 .
.
【解析】
试题分析:(Ⅰ)将函数 去掉绝对值写成分段函数形式,结合函数图像满足
去掉绝对值写成分段函数形式,结合函数图像满足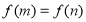 的
的 只可能为
只可能为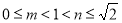 ,从而
,从而 ,
,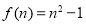 ,由
,由 即可得
即可得 ;(Ⅱ)写出
;(Ⅱ)写出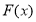 的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为
的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为 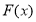 的最小值;(Ⅲ)将
的最小值;(Ⅲ)将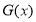 写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.
写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.
试题解析:(Ⅰ)
由 图像可知,
图像可知,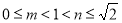
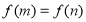 即为
即为 ,所以
,所以 3分
3分
(Ⅱ)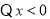 ,则
,则 ,
,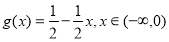
当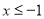 时,
时,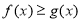 ,即为
,即为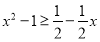 ,解得
,解得
当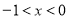 时,
时, ,即为
,即为 ,解得
,解得

当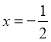 时,
时,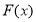 最小值为
最小值为
(本问也可直接利用图像说明理由求解) 6分
(Ⅲ)

①记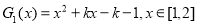 ,结合图像可知,
,结合图像可知,
当 ,即
,即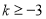 时,
时,
当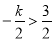 ,即
,即 时,
时,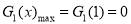 8分
8分
②记 ,结合图像可知,
,结合图像可知,
当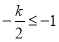 ,即
,即 时,
时,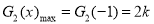
当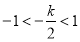 ,即
,即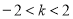 时,
时,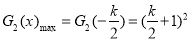
当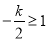 ,即
,即 时,
时,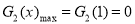
③记 ,结合图像可知,
,结合图像可知,
当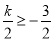 ,即
,即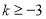 时,
时,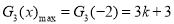
当 ,即
,即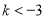 时,
时,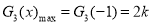 10分
10分
由上讨论可知:
当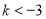 时,
时,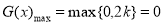
当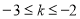 时,
时,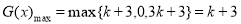
当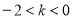 时,
时,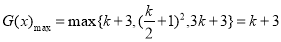
当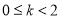 时,
时,
当 时,
时,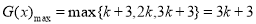 15分
15分
综上所述:当 时,
时, 在
在 上的最大值为0
上的最大值为0
当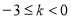 时,
时, 在
在 上的最大值为
上的最大值为
当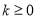 时,
时, 在
在 上的最大值为
上的最大值为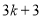 . 16分
. 16分
考点:分段函数的解析式求法,数形结合思想,分类讨论思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目