题目内容
(本小题满分10分).
(选修4-1)
如图,在 中,
中, ,以
,以 为直径的圆
为直径的圆 交
交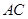 于点
于点 ,设
,设 为
为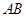 的中点.
的中点.

(I)求证:直线 为圆
为圆 的切线;
的切线;
(Ⅱ)设 交圆
交圆 于点
于点 ,求证:
,求证:
【答案】
见解析。
【解析】(I)先连接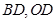 ,易知
,易知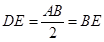 ,进一步得到
,进一步得到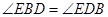 ,
,
再由等腰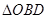 中,
中,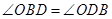 ,然后可得
,然后可得 ,问题得证.
,问题得证.
(II) 证明本题的关键是证明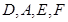 四点共圆,然后根据同旁内角互补四点共圆即可.
四点共圆,然后根据同旁内角互补四点共圆即可.
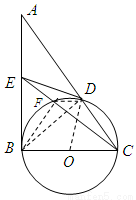
证明:(Ⅰ)连接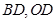
在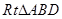 中,
中,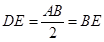
则有在等腰 中,
中,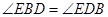 …… 2分
…… 2分
在等腰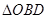 中,
中,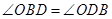
可得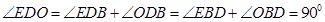
即直线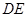 为圆
为圆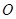 的切线 …… 5分
的切线 …… 5分
(Ⅱ)连接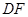 ,则有
,则有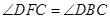 , …… 6分
, …… 6分
又因为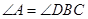 , 可得
, 可得 则有
则有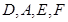 四点共圆…… 8分
四点共圆…… 8分
因此得到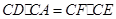 …… 10分
…… 10分

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,