题目内容
已知f(x)=a1x+a2x2+a3x3+……+anxn ,n为正偶数,且a1 ,a2 ,a3, ……,
an组成等差数列,又f(1)=n2 ,f(-1)=n ,试比较f(![]() )与3的大小
)与3的大小![]()
f(![]() )<3
)<3
解析:
∵f(1)=n2 ,f(-1)=n ,
∴f(1)=a1 +a2+……+an=n2 , f(-1)=-a1+a2-a3+a4-a5+……-an-1+an=n
依题设有![]() ,
,![]() d=n
d=n
∴d=2, a1=1
于是![]()
∴f(x)=x+3x2+5x3+7x4+……+(2n-1)xn
∴f(![]() )=
)=![]() +3(
+3(![]() )2+5(
)2+5(![]() )3+7(
)3+7(![]() )4+……+(2n-1)(
)4+……+(2n-1)(![]() )n……①
)n……①
两边同乘![]() :
:![]() f(
f(![]() )=
)=![]() +3(
+3(![]() )3+5(
)3+5(![]() )4+7(
)4+7(![]() )5+……+(2n-1)(
)5+……+(2n-1)(![]() )n+1…②
)n+1…②
①-②得 ![]() f(
f(![]() )=
)=![]() +2(
+2(![]() )2+2(
)2+2(![]() )3+……+2(
)3+……+2(![]() )n-(2n-1)(
)n-(2n-1)(![]() )n+1
)n+1
即![]() f(
f(![]() )=
)=![]() +
+![]() +(
+(![]() )2+……+(
)2+……+(![]() )n-1-(2n-1)(
)n-1-(2n-1)(![]() )n+1
)n+1
∴f(![]() )=1+1+
)=1+1+![]() +
+![]() +……+
+……+![]() -(2n-1)(
-(2n-1)(![]() )n
)n
=1+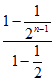 -(2n-1)
-(2n-1)![]() = 1+2-
= 1+2-![]() -(2n-1)
-(2n-1)![]() <3
<3
∴f(![]() )<3
)<3

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.
,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.