题目内容
(理)已知函数f(x)=ln(x+(1)求函数f(x)的单调区间;
(2)如果关于x的方程g(x)=![]() x+m有实数根,求实数m的取值范围;
x+m有实数根,求实数m的取值范围;
(3)是否存在正数k,使得关于x的方程f(x)=kg(x)有两个不相等的实数根?如果存在,求k满足的条件;如果不存在,说明理由.
(文)已知f(x)=a1x+a2x2+a3x3+…+anxn(n∈N*)满足f(1)=n2.
(1)求数列{an}的通项公式,并指出数列为何数列;
(2)求证:![]() <f(
<f(![]() )<3(n>2,n∈N*).
)<3(n>2,n∈N*).
答案:(理)(1)函数f(x)的定义域是(![]() ,0)∪(0,+∞).
,0)∪(0,+∞).
对f(x)求导得f′(x)=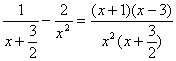
由f′(x)>0,得![]() <x<-1或x>3
<x<-1或x>3
由f′(x)<0,得-1<x<0或0<x<3.
因此(![]() ,-1)和(3,+∞)是函数f(x)的增区间;
,-1)和(3,+∞)是函数f(x)的增区间;
(-1,0)和(0,3)是函数f(x)的减区间.
(2)解法一:因为g(z)=![]() x+m
x+m![]() lnx=
lnx=![]() x+m
x+m![]() m=lnx
m=lnx![]() x.
x.
所以实数m的取值范围就是函数φ(x)=lnx![]() x的值域
x的值域
对φ(x)求导得φ′(x)=![]() .
.
令φ′(x)=0,得x=2,并且当x>2时,φ′(x)<0;
当0<x<2时,φ′(x)>0
∴当x=2时,φ(x)取得最大值,且φ(x)max=φ(2)=ln2-1.
又当x无限趋近于0时,lnx无限趋近于-∞,![]() 无限趋近于0,
无限趋近于0,
进而有φ(x)=lnx![]() 无限趋近于-∞.
无限趋近于-∞.
因此,函数φ(x)=lnx![]() 的值域是(-∞,ln2-1)
的值域是(-∞,ln2-1)
即实数m的取值范围是(-∞,ln2-1).
解法二:方程g(x)=![]() x+m有实数根等价于直线g(x)=
x+m有实数根等价于直线g(x)=![]() x+m与曲线y=lnx有公共点,并且当直线g(x)=
x+m与曲线y=lnx有公共点,并且当直线g(x)=![]() x+m与曲线y=lnx相切时,m取得最大值.
x+m与曲线y=lnx相切时,m取得最大值.
设直线y=![]() x+t与曲线y=lnx相切,切点为T(x0,y0).
x+t与曲线y=lnx相切,切点为T(x0,y0).
则对y=lnx求导得y′=![]() ,根据相切关系得
,根据相切关系得
解得x0=2,y0=ln2,进而t=ln2-1.
所以m的最大值是ln2-1.而且易知当m≤ln2-1时,直线y=![]() x+m与曲线y=lnx总有公共点.
x+m与曲线y=lnx总有公共点.
因此,实数m的取值集合是(-∞,ln2-1).
(3)这样的正数k不存在.
下面采用反证法来证明:假设存在正数k,使得关于x的方程f(x)=kg(x)有两个不相等的实数根x1和x2,则

根据对数函数定义域知x1和x2都是正数.
又由(1)可知,当x>0时,f(x)min=ln(3+![]() )+
)+![]() >0
>0
∴f(x1)=ln(x1+![]() )+
)+![]() >0,
>0,
f(x2)=ln(x2+![]() )+
)+![]() >0.
>0.
再由k>0,可得g(x1)=lnx1>0,g(x2)=lnx2>0![]() x1>1,x2>1.
x1>1,x2>1.
由于x1![]() x2,所以不妨设1<x1<x2
x2,所以不妨设1<x1<x2
由①和②可得
利用比例性质得

即 (*)
(*)
由于lnx是区间(1,+∞)上的恒正增函数,且1<x1<x2,∴![]() <1.
<1.
又由于ln(1+![]() )+
)+![]() 是区间(1,+∞)上的恒正减函数,且1<x1<x2.
是区间(1,+∞)上的恒正减函数,且1<x1<x2.
∴ .
.
∴
这与(*)式矛盾.
因此,满足条件的正数k不存在.
(文)(1)由f(1)=n2得:a1+a2+…+an=n2,
当n=1时,a1=1
当n≥2时,an=(a1+a2+…+an)-(a1+a2+…+an)=n2-(n-1)2=2n-1
所以,an=2n-1,数列是等差数列.
(2)∵![]() ①
①
![]() ②
②
①-②,得
![]()
=
=![]()
∴f(![]() )=3
)=3![]() <3
<3
令g(n)=3![]() ,当n>2且n∈N*时
,当n>2且n∈N*时
∵g(n+1)-g(n)=![]()
∵n>2,∴![]() >0,
>0,![]() >0,∴g(n+1)>g(n)
>0,∴g(n+1)>g(n)
∴g(n)是关于n(n>2,n∈N*)的递增数列,即g(2)<g(3)<…<g(n),
而g(2)=![]() ,∴
,∴![]() <
<![]() <3(n>2,n∈N*)成立.
<3(n>2,n∈N*)成立.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
 (理)已知函数
(理)已知函数 (2011•普陀区三模)(理)已知函数
(2011•普陀区三模)(理)已知函数