题目内容
已知f(x)=a1x+a2x2+a3x3+…+anxn，且al，a2，a3，…，an组成等差数列，n为正偶数，又f(1)=n2，f(-1)=n．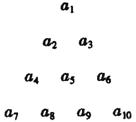
(1)求数列{an}的通项公式；
(2)将数列{an}的各项排成三角形状(如图)，记A(i，j)为第i行第j个数，例如：A(4，3)=a9，求A(10，1)+A(10，2)+…+A(10，10)；
(3)比较f(
)与3的大小.
解：(1)由f(1)=n2得：a1+a2+…+an=n2
由f(-1)=n得：-a1+a2-…+an=n
∴a1+a3+…an-1=
a2+a4+…+an=，设公差为d，
两式相减得：
d=n
d=2，又a1=1，∴an=2n-1．
(2)第10行前(不包括第10行)共1+2+3+3+4+5+6+7+8+9=45个数
∵A(10，1)=a46=2×46-1=91
∴ A(10，1)+A(10，2)+A(10，3)+A(10，4)+A(10，5)+A(10，6)+A(10，7)+A(10，8)+A(10，9)+A(10，10)=10a46+
×10×9×d=1 000
(3)f（
）=1×
+3×（
）2+5×（
）3+…+(2n-1)（
）n
错位相减得：f(
)=3-(2n+3)×（
）n＜3
练习册系列答案
科学实验活动册系列答案
相关题目
)与3的大小
＜f(
)＜3(n＞2).
,cn=
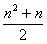,Tn为数列{cn}的前n项和，若Tn＜λ(bn+1+1)，对一切n∈N*都成立，试求λ的取值范围．
)+
，g(x)=lnx．
x+m有实数根，求实数m的取值范围；
＜f(
)＜3(n＞2，n∈N*)．