题目内容
【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1,f(x)=x2 . 如果函数g(x)=f(x)﹣(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z)
B.2k或2k+ ![]() (k∈Z)
(k∈Z)
C.0
D.2k或2k﹣ ![]() (k∈Z)
(k∈Z)
【答案】D
【解析】解:由g(x)=f(x)﹣(x+m)=0得f(x)=(x+m).设y=f(x),y=x+m. 因为f(x)是定义在R上且周期为2的偶函数,所以当﹣1≤x≤1时,f(x)=x2 . ①由图象可知当直线y=x+m经过点O(0,0)时,直线y=x+a与y=f(x)恰有两个公共点,此时m=0,由于函数f(x)是周期为2的函数,所以当m=2k时(k∈Z),
直线y=x+m与曲线y=f(x)恰有两个公共点.②由图象可知直线y=x+m与f(x)=x2相切时,直线y=x+m与曲线y=f(x)也恰有两个公共点.
f'(x)=2x,由f'(x)=2x=1,解得x= ![]() ,所以y=
,所以y= ![]() ,即切点为(
,即切点为( ![]() ),
),
代入直线y=x+m得m= ![]() .
.
由于函数f(x)是周期为2的函数,所以当m= ![]() 时(k∈Z),直线y=x+m与曲线y=f(x)恰有两个公共点.
时(k∈Z),直线y=x+m与曲线y=f(x)恰有两个公共点.
综上满足条件的实数m的值为m=2k或m= ![]() 时(k∈Z).
时(k∈Z).
故选D.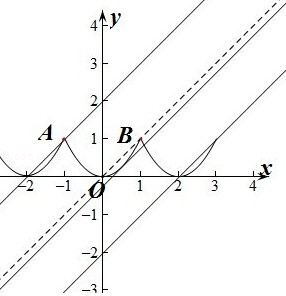
利用函数是周期为2的偶函数,作出函数y=f(x)的图象,利用直线y=x+m与曲线y=f(x)恰有两个公共点,利用数形结合的思想求m的值.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
