题目内容
已知函数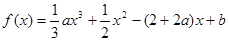 (
(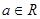 )
)
(1)若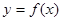 在点
在点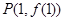 处的切线方程为
处的切线方程为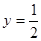 ,求
,求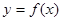 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)若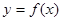 在
在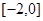 上存在极值点,求实数
上存在极值点,求实数 的取值范围.
的取值范围.
(1)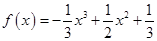 ,单调递减区间有
,单调递减区间有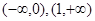 ;(2)
;(2)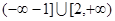
解析试题分析:(1)由题设知,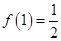 ,
,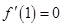 解方程组可得
解方程组可得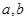 的值,进而确定函数
的值,进而确定函数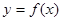 的解析式及其导数的表达式
的解析式及其导数的表达式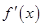 ,并由不等式
,并由不等式 的解得到函数据的单调递减区间.
的解得到函数据的单调递减区间.
(2)函数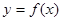 在
在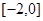 上存在极值点
上存在极值点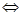 导函数
导函数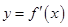 在
在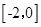 上存在零点,且零点两侧导数值异号,因为,导函数的二次项系数为
上存在零点,且零点两侧导数值异号,因为,导函数的二次项系数为 ,所以要分
,所以要分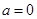 与
与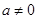 两种情詋进行讨论,后者为一元二次方程的分布问题.
两种情詋进行讨论,后者为一元二次方程的分布问题.
试题解析: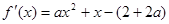
(1)由已知可得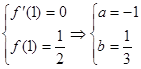
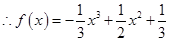
此时 , 4分
, 4分
由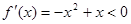 得
得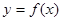 的单调递减区间为
的单调递减区间为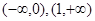 ; 7分
; 7分
(2)由已知可得 在
在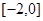 上存在零点且在零点两侧
上存在零点且在零点两侧 值异号
值异号
⑴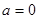 时,
时,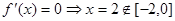 ,不满足条件;
,不满足条件;
⑵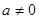 时,可得
时,可得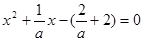 在
在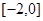 上有解且
上有解且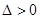
设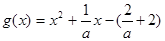
①当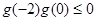 时,满足
时,满足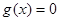 在
在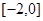 上有解
上有解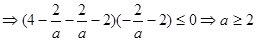 或
或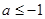 此时满足
此时满足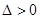
②当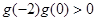 时,即
时,即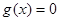 在
在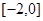 上有两个不同的实根
上有两个不同的实根
则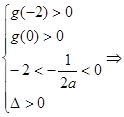
 无解
无解
综上可得实数 的取值范围为
的取值范围为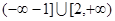 . 14分
. 14分
考点:1、导数的几何意;2、导数在研究函数单调性与极值等性质中的应用;3、二次函数与一元二次方程.

练习册系列答案
相关题目
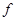 (
( ) =
) =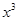 ,g (
,g (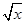 。
。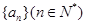 满足
满足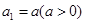 ,
,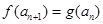 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的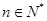 ,都有
,都有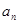 ≤
≤ 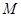 .
.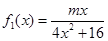 ,
,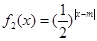 ,其中m∈R.
,其中m∈R.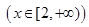 的单调性,并证明你的结论;
的单调性,并证明你的结论;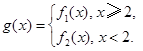 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.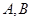 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.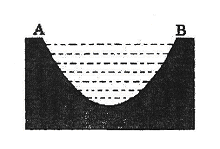
 与日产量
与日产量 (件)之间近似地满足关系式
(件)之间近似地满足关系式 (日产品废品率
(日产品废品率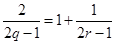
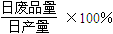 ).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润
).已知每生产一件正品可赢利2千元,而生产一件废品则亏损1千元.(该车间的日利润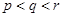 日正品赢利额
日正品赢利额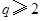 日废品亏损额)
日废品亏损额)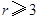 (千元)表示为日产量
(千元)表示为日产量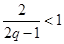 (件)的函数;
(件)的函数;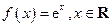 .
.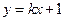 与
与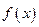 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值;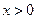 ,讨论曲线
,讨论曲线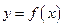 与曲线
与曲线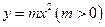 公共点的个数;
公共点的个数;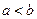 ,比较
,比较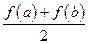 与
与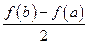 的大小,并说明理由.
的大小,并说明理由.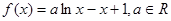 .
. 的单调区间;
的单调区间;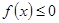 在
在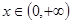 上恒成立,求所有实数
上恒成立,求所有实数 的值;
的值;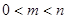 ,证明:
,证明: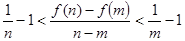
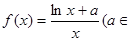 R).
R).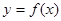 在点
在点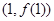 处的切线与直线
处的切线与直线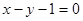 平行,求
平行,求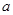 的值;
的值; 的单调区间和极值;
的单调区间和极值;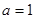 ,且
,且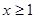 时,证明:
时,证明: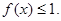
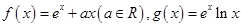 (e为自然对数的底数).
(e为自然对数的底数).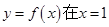 处的切线为
处的切线为 ,若
,若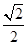 ,求a的值;
,求a的值;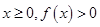 恒成立,试确定
恒成立,试确定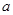 的取值范围;
的取值范围;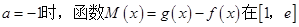 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.