题目内容
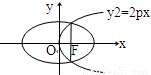
 如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
分析:设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',可得Rt△AFF'中,AF=FF'=p,从而AF'=
p,再根据椭圆的定义,可得AF+AF'=2a=(1+
)p,最后用椭圆的离心率的公式求出该椭圆的离心率.
| 2 |
| 2 |
解答:解: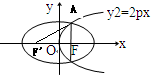 设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',
设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',
∴F(
,0),F'(-
,0),可得焦距FF'=p=2c,(c=
为椭圆的半焦距)
对抛物线方程y2=2px令x=
,得y2=p2,所以AF=|yA|=p
∴Rt△AFF'中,AF=FF'=p,可得AF'=
p
再根据椭圆的定义,可得AF+AF'=2a=(1+
)p,
∴该椭圆的离心率为e=
=
=
=
-1
故答案为:
-1
 设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',
设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',∴F(
| p |
| 2 |
| p |
| 2 |
| a2-b2 |
对抛物线方程y2=2px令x=
| p |
| 2 |
∴Rt△AFF'中,AF=FF'=p,可得AF'=
| 2 |
再根据椭圆的定义,可得AF+AF'=2a=(1+
| 2 |
∴该椭圆的离心率为e=
| c |
| a |
| 2c |
| 2a |
| p | ||
(1+
|
| 2 |
故答案为:
| 2 |
点评:本题给出椭圆的右焦点恰好是抛物线的焦点,并且两曲线的通径合在一起,求椭圆的离心率,着重考查了椭圆的定义与简单几何性质和抛物线的标准方程等知识点,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图所示,已知抛物线
如图所示,已知抛物线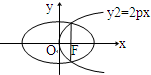
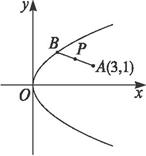
 的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .
的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .