题目内容
（本小题满分12分）
如图，在三棱锥S－ABC中，BC⊥平面SAC，AD⊥SC．
（I）求证：AD⊥平面SBC；
（II）试在SB上找一点E，使得BC//平面ADE，并证明你的结论．
【答案】
（I）见解析；（II）过D作DE//BC，交SB于E
【解析】（I）通过证明BC⊥AD，通过AD⊥SC，BC∩SC=C，证明AD⊥平面SBC；
（II）过D作DE∥BC，交SB于E，E点即为所求．直接利用直线与平面平行的判定定理即可证明BC∥平面ADE．
（I）证明：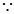
BC⊥平面SAC，
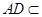平面SAC，∴BC⊥AD，
又∵AD⊥SC，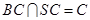
，
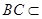平面SBC，
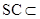平面SBC，∴AD⊥平面SBC．
…………（5分）
（II）过D作DE//BC，交SB于E，E点即为所求．
∵BC//DE，BC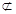
面ADE，DE
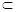平面ADE，
∴BC//平面ADE． …………（10分）
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
