题目内容
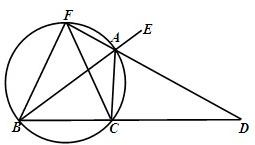 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.(1)求证:FB=FC;
(2)求证:FB2=FA•FD;
(3)若AB是△ABC外接圆的直径,且∠EAC=120°,BC=6,求AD的长.
分析:(1)两线段在同一个三角形中,故可以用证两底角相等,通过等边对等角来证两边相等;
(2)由图形知,可以证明△FBA∽△FDB,由于角BFD是公共角,再证明角FAB与角FBD相等即可证出两三角形相似;
(3)由题设条件可求得三角形ABC与三角形ACD的内角,又此两三角形都是直角三角形,故可借助直角三角形中的相关知识求AD的长.
(2)由图形知,可以证明△FBA∽△FDB,由于角BFD是公共角,再证明角FAB与角FBD相等即可证出两三角形相似;
(3)由题设条件可求得三角形ABC与三角形ACD的内角,又此两三角形都是直角三角形,故可借助直角三角形中的相关知识求AD的长.
解答:解:(1)因为∠EAC=∠ABC+∠ACB=∠ABC+∠BCF+∠ACF=∠ABC+∠BCF+∠ABF=∠BCF+∠FBC
又∠EAC=2∠FAB=2∠BCF
所以∠FCB=∠FBC,
所以FB=FC,(3分)
(2)因为在△FBA∽△FDB中,∠BFD是公共角,
由于同弦所对的圆周角相等,故∠FAB等于∠FCB,又由(1)∠FCB=∠FBC
故可得∠FBC=∠FAB
所以△FBA∽△FDB,所以
=
,整理得FB2=FA•FD(6分)
(3)∠EAC=120°,所以∠BAC=60°
因为AB为直径,所以∠ACB=90°,
∴∠ABC=30°,
又∠DAC=60°,∠ACD=90°,可得∠ADC=30°
在直角三角形ABC中,由于BC=6,所以AC=2
在直角三角形ADC中,可得AD=4
(10分)
又∠EAC=2∠FAB=2∠BCF
所以∠FCB=∠FBC,
所以FB=FC,(3分)
(2)因为在△FBA∽△FDB中,∠BFD是公共角,
由于同弦所对的圆周角相等,故∠FAB等于∠FCB,又由(1)∠FCB=∠FBC
故可得∠FBC=∠FAB
所以△FBA∽△FDB,所以
| FB |
| FD |
| FA |
| FB |
(3)∠EAC=120°,所以∠BAC=60°
因为AB为直径,所以∠ACB=90°,
∴∠ABC=30°,
又∠DAC=60°,∠ACD=90°,可得∠ADC=30°
在直角三角形ABC中,由于BC=6,所以AC=2
| 3 |
在直角三角形ADC中,可得AD=4
| 3 |
点评:本题考点是与圆有关的比例线段,考查圆中同弦所对的圆周角相等及切割线定理以及直角三角形中边角的转化,此类题对思维灵活性要求较高,需要答题者熟悉题设条件与相关图形的结构,然后组合出解决问题的方案,解题时注意体会本题的这一特征,此也是几何证明题共有的特征.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2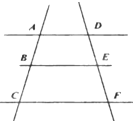 如图,已知AD∥BE∥CF,下列比例式成立的是( )
如图,已知AD∥BE∥CF,下列比例式成立的是( ) 如图,已知长方体ABCD-A′B′C′D′中,AB=2
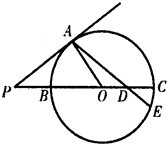
如图,已知长方体ABCD-A′B′C′D′中,AB=2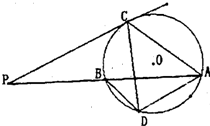 (2011•洛阳二模)如图,已知PBA是圆O的割线,PC是圆的切线,
(2011•洛阳二模)如图,已知PBA是圆O的割线,PC是圆的切线,