题目内容
在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足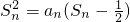 .
.
(1)求an;
(2)令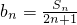 ,求数列{bn}的前项和Tn.
,求数列{bn}的前项和Tn.
解:(1)当n≥2时,an=Sn-Sn-1,
∴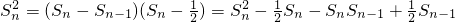 ,
,
∴Sn-1-Sn=2SnSn-1,
∴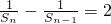 ,
,
即数列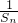 为等差数列,S1=a1=1,
为等差数列,S1=a1=1,
∴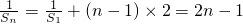 ,
,
∴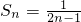 ,…(4分)
,…(4分)
当n≥2时,an=sn-sn-1=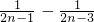 =
=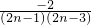
∴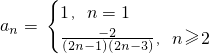 …(8分)
…(8分)
(2)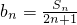 =
=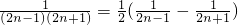 ,
,
∴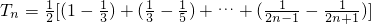 =
=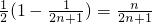
分析:(1)当n≥2时,由an=Sn-Sn-1,代入已知整理可得Sn-1-Sn=2SnSn-1,即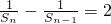 ,结合等差数列的通项公式可求Sn,进而可求当n≥2时an,在对n=1时求a1,从而可求an
,结合等差数列的通项公式可求Sn,进而可求当n≥2时an,在对n=1时求a1,从而可求an
(2)由于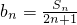 =
=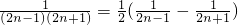 ,考虑利用裂项求和即可
,考虑利用裂项求和即可
点评:本题主要考查了利用递推公式 求解数列的通项公式,要注意对n=1的检验是做题中容易漏掉的知识点,还考查了裂项求和方法的应用.
求解数列的通项公式,要注意对n=1的检验是做题中容易漏掉的知识点,还考查了裂项求和方法的应用.
∴
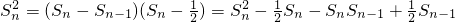 ,
,∴Sn-1-Sn=2SnSn-1,
∴
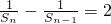 ,
,即数列
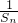 为等差数列,S1=a1=1,
为等差数列,S1=a1=1,∴
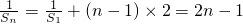 ,
,∴
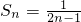 ,…(4分)
,…(4分)当n≥2时,an=sn-sn-1=
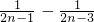 =
=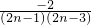
∴
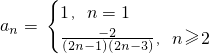 …(8分)
…(8分)(2)
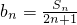 =
=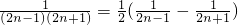 ,
,∴
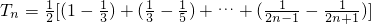 =
=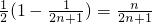
分析:(1)当n≥2时,由an=Sn-Sn-1,代入已知整理可得Sn-1-Sn=2SnSn-1,即
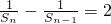 ,结合等差数列的通项公式可求Sn,进而可求当n≥2时an,在对n=1时求a1,从而可求an
,结合等差数列的通项公式可求Sn,进而可求当n≥2时an,在对n=1时求a1,从而可求an(2)由于
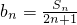 =
=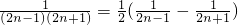 ,考虑利用裂项求和即可
,考虑利用裂项求和即可点评:本题主要考查了利用递推公式
 求解数列的通项公式,要注意对n=1的检验是做题中容易漏掉的知识点,还考查了裂项求和方法的应用.
求解数列的通项公式,要注意对n=1的检验是做题中容易漏掉的知识点,还考查了裂项求和方法的应用. 
练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.