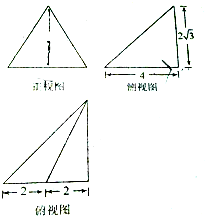
题目内容
13.已知函数f(x)=lnx-a(1-$\frac{1}{x}$),a∈R.(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)的最小值为0.
(i)求实数a的值;
(ii)已知数列{an}满足:a1=1,an+1=f(an)+2,记[x]表示不大于x的最大整数,求证:n>1时[an]=2.
分析 (Ⅰ)利用导数,对a讨论,当a≤0时,当a>0时,即可求得f(x)的单调区间;
(Ⅱ)(i)利用(Ⅰ)的结论即可求得a的值;
(ii)利用归纳推理,猜想当n≥3,n∈N时,2<an<$\frac{5}{2}$,利用数学归纳法证明,即可得出结论.
解答 解:(Ⅰ)函数f(x)的定义域为(0,+∞),且f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$.
当a≤0时,f′(x)>0,所以f(x)在区间(0,+∞)内单调递增;
当a>0时,由f′(x)>0,解得x>a;由f′(x)<0,解得0<x<a.
所以f(x)的单调递增区间为(a,+∞),单调递减区间为(0,a).
综上述:a≤0时,f(x)的单调递增区间是(0,+∞);
a>0时,f(x)的单调递减区间是(0,a),单调递增区间是(a,+∞).
(Ⅱ)(ⅰ)由(Ⅰ)知,当a≤0时,f(x)无最小值,不合题意;
当a>0时,[f(x)]min=f(a)=1-a+lna=0,
令g(x)=1-x+lnx(x>0),则g′(x)=-1+$\frac{1}{x}$=$\frac{1-x}{x}$,
由g′(x)>0,解得0<x<1;由g′(x)<0,解得x>1.
所以g(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
故[g(x)]max=g(1)=0,即当且仅当x=1时,g(x)=0.
因此,a=1.
(ⅱ)因为f(x)=lnx-1+$\frac{1}{x}$,所以an+1=f(an)+2=1+$\frac{1}{{a}_{n}}$+lnan.
由a1=1得a2=2于是a3=$\frac{3}{2}$+ln2.因为$\frac{1}{2}$<ln2<1,所以2<a3<$\frac{5}{2}$.
猜想当n≥3,n∈N时,2<an<$\frac{5}{2}$.
下面用数学归纳法进行证明.
①当n=3时,a3=$\frac{3}{2}$+ln2,故2<a3<$\frac{5}{2}$.成立.
②假设当n=k(k≥3,k∈N)时,不等式2<ak<$\frac{5}{2}$成立.
则当n=k+1时,ak+1=1+$\frac{1}{{a}_{k}}$+lnak,
由(Ⅰ)知函数h(x)=f(x)+2=1+$\frac{1}{x}$+lnx在区间(2,$\frac{5}{2}$)单调递增,
所以h(2)<h(ak)<h($\frac{5}{2}$),又因为h(2)=1+$\frac{1}{2}$+ln2>2,
h($\frac{5}{2}$)=1+$\frac{2}{5}$+ln$\frac{5}{2}$<1+$\frac{2}{5}$+1<$\frac{5}{2}$.
故2<ak+1<$\frac{5}{2}$成立,即当n=k+1时,不等式成立.
根据①②可知,当n≥3,n∈N时,不等式2<an<$\frac{5}{2}$成立.
综上可得,n>1时[an]=2.
点评 本题主要考查函数的导数、导数的应用等基础知识,考查推理论证能力、运算求解能力、创新意识等,
考查函数与方程思想、化归与转化思想、分类与整合思想、有限与无限思想等,属难题.

| A. | 若m∥α,n∥α,m∥n | B. | 若m∥α,m∥β,α∥β | C. | 若α⊥γ,β⊥γ,α∥β | D. | 若m⊥α,n?α,m⊥n |
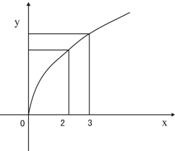 函数f(x)的图象如图,f′(x)是f(x)的导函数,则下列数值排列正确的是( )
函数f(x)的图象如图,f′(x)是f(x)的导函数,则下列数值排列正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f(3)-f(2)<f′(2)<f′(3) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f′(3)<f(3)-f(2)<f′(2) |
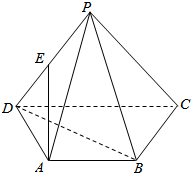 如图,在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥CD,∠ADC=$\frac{π}{3}$,PD=PC=CD=2AB=2,E为PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥CD,∠ADC=$\frac{π}{3}$,PD=PC=CD=2AB=2,E为PD的中点