题目内容
已知f(x)是定义在[-1,1]上的偶函数,且在(0,1]上单调递增,则不等式f(1-x)<f(x2-1)的解集是
- A.(-2,1)
- B.
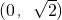
- C.(0,1)∪
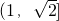
- D.不能确定
C
分析:由f(x)是定义在[-1,1]上,可得:-1≤1-x≤1①;-1≤x2-1≤1②;f(x)是定义在[-1,1]上的偶函数,(0,1]上单调递增,可得|1-x|<|x2-1|③;x=0时,有f(0)<f(0),矛盾,故|x|≠0④,由①②③④可得不等式组,解之即可得到答案.
解答:∵f(x)是定义在[-1,1]上的偶函数,且在(0,1]上单调递增,∴f(1-x)<f(x2-1)?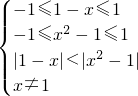 解得:
解得: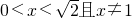 ;
;
∴不等式f(1-x)<f(x2-1)的解集为: .
.
故选C.
点评:本题考察函数奇偶性的性质,难点在求不等式组的解集,易错点在于忽略隐含条件x≠1,属于中档题.
分析:由f(x)是定义在[-1,1]上,可得:-1≤1-x≤1①;-1≤x2-1≤1②;f(x)是定义在[-1,1]上的偶函数,(0,1]上单调递增,可得|1-x|<|x2-1|③;x=0时,有f(0)<f(0),矛盾,故|x|≠0④,由①②③④可得不等式组,解之即可得到答案.
解答:∵f(x)是定义在[-1,1]上的偶函数,且在(0,1]上单调递增,∴f(1-x)<f(x2-1)?
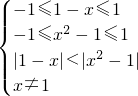 解得:
解得: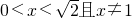 ;
;∴不等式f(1-x)<f(x2-1)的解集为:
 .
.故选C.
点评:本题考察函数奇偶性的性质,难点在求不等式组的解集,易错点在于忽略隐含条件x≠1,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目