题目内容
(1)指出下列两个函数的奇偶性①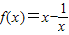 ;②y=x2-3|x|+2
;②y=x2-3|x|+2(2)已知函数f(x)=-x2+mx-2是偶函数,求m的值;
(3)已知函数g(x)=ax3-bx+3,且g(-2)=5,求g(2)的值.
【答案】分析:(1)先求函数的定义域,再求出f(-x)和f(x)的关系,根据奇(偶)函数的定义判断;
(2)根据偶函数的定义知f(1)=f(-1),代入解析式求出m的值;
(3)令h(x)=ax3-bx判断出是奇函数,列出g(2)和g(-2)的方程,根据题意和奇函数的关系式求出g(2)的值.
解答:解:(1)∵ 的定义域是{x|x≠0},f(-x)=-x-
的定义域是{x|x≠0},f(-x)=-x- =-f(x),
=-f(x),
∴函数f(x)是奇函数;
∵y=x2-3|x|+2的定义域是R,且有(-x)2-3|-x|+2=x2-3|x|+2,
∴此函数是偶函数.
(2)∵函数f(x)=-x2+mx-2是偶函数,∴f(1)=f(-1),
即-1+m-2=-1-m-2,解得m=0.
(3)∵函数h(x)=ax3-bx的定义域是R,且h(-x)=-ax3+bx=-h(x),
∴函数h(x)是奇函数,则h(2)=-h(-2),
∵g(2)=h(2)+3 ①,g(-2)=h(-2)+3=5 ②,
∴①+②得,g(2)=1.
点评:本题的考点是函数奇偶性的判断和应用,由定义判断函数奇偶性必须先求出定义域,对于利用奇偶性求值,即利用关系式“f(x)=f(-x)”“f(x)=-f(-x)”求函数值.
(2)根据偶函数的定义知f(1)=f(-1),代入解析式求出m的值;
(3)令h(x)=ax3-bx判断出是奇函数,列出g(2)和g(-2)的方程,根据题意和奇函数的关系式求出g(2)的值.
解答:解:(1)∵
 的定义域是{x|x≠0},f(-x)=-x-
的定义域是{x|x≠0},f(-x)=-x- =-f(x),
=-f(x),∴函数f(x)是奇函数;
∵y=x2-3|x|+2的定义域是R,且有(-x)2-3|-x|+2=x2-3|x|+2,
∴此函数是偶函数.
(2)∵函数f(x)=-x2+mx-2是偶函数,∴f(1)=f(-1),
即-1+m-2=-1-m-2,解得m=0.
(3)∵函数h(x)=ax3-bx的定义域是R,且h(-x)=-ax3+bx=-h(x),
∴函数h(x)是奇函数,则h(2)=-h(-2),
∵g(2)=h(2)+3 ①,g(-2)=h(-2)+3=5 ②,
∴①+②得,g(2)=1.
点评:本题的考点是函数奇偶性的判断和应用,由定义判断函数奇偶性必须先求出定义域,对于利用奇偶性求值,即利用关系式“f(x)=f(-x)”“f(x)=-f(-x)”求函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ;②y=x2-3|x|+2
;②y=x2-3|x|+2