题目内容
已知x∈R,且f(x+1)=-f(x),则f(x+2)=-f(x+1)=-[-f(x)]=f(x),得f(x)的一个周期为2.类比上述结论,请写出下列两个函数的一个周期:(1)已知a为正常数,x∈R,且f(x+a)=-f(x),则f(x)的一个周期为
(2)已知a为正常数,x∈R,且f(x+a)=
| f(x)-1 | f(x)+1 |
分析:(1)根据周期函数的定义,f(x+T)=f(x),T周期,先将f(x+a)=-f(x)转化成f(x+2a)=-f(x+a)=f(x),根据函数的周期性的定义可知该函数的周期.
(2)根据周期函数的定义,依次计算f(x+na)(n∈N+)直到等于f(x)为止.
(2)根据周期函数的定义,依次计算f(x+na)(n∈N+)直到等于f(x)为止.
解答:解:(1)∵f(x+a)=-f(x),
∴f(x+2a)=-f(x+a)=f(x)即f(x+2a)=f(x)
∴函数f(x)的周期是2a.
(2)∵f(x+2a)=
=-
,∴f(x+3a)=
=
,∴f(x+4a)=
=f(x);
∴f(x)的周期为4a.
故答案为:2a;4a.
∴f(x+2a)=-f(x+a)=f(x)即f(x+2a)=f(x)
∴函数f(x)的周期是2a.
(2)∵f(x+2a)=
| f(x+a)-1 |
| 1+f(x+a) |
| 1 |
| f(x) |
| f(2a)-1 |
| 1+f(2a) |
| f(x)-1 |
| f(x)+1 |
| f(3a)-1 |
| 1+f(3a) |
∴f(x)的周期为4a.
故答案为:2a;4a.
点评:本题考查了类比推理、抽象函数的周期性,利用周期函数的定义求解,一定要抓牢基础,要求平时学习掌握知识要扎实,灵活,属于基础题.

练习册系列答案
相关题目
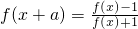 ,则f(x)的一个周期为________.
,则f(x)的一个周期为________. ,则f(x)的一个周期为 .
,则f(x)的一个周期为 .