题目内容
(2012•许昌一模)某次体育比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲,乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
若甲队横扫对手获胜(即3:0获胜)的概率是
,比赛至少打满4场的概率为
(Ⅰ)求p,q的值;
(Ⅱ)求甲队获胜场数的分布列和数学期望.
| 出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 | ||||||
| 获胜概率 |
|
p | q |
|
|
| 1 |
| 8 |
| 3 |
| 4 |
(Ⅰ)求p,q的值;
(Ⅱ)求甲队获胜场数的分布列和数学期望.
分析:(Ⅰ)利用甲队横扫对手获胜(即3:0获胜)的概率是
,比赛至少打满4场的概率为
,建立方程组,即可求p,q的值;
(Ⅱ)求得甲队获胜场数的可能取值,求出相应的概率,可得分布列和数学期望.
| 1 |
| 8 |
| 3 |
| 4 |
(Ⅱ)求得甲队获胜场数的可能取值,求出相应的概率,可得分布列和数学期望.
解答:解:(Ⅰ)由题意
∴p=q=
;
(Ⅱ)设甲队获胜场数为ξ,则ξ的可取的值为0,1,2,3
P(ξ=0)=(
)3=
;P(ξ=1)=
•
•(
)2•
=
;
P(ξ=2)=
•(
)2•(
)2•
=
;P(ξ=3)=(
)3+
•
•(
)2•
+
•(
)2•(
)2•
=
∴ξ的分布列为
Eξ=0×
+1×
+2×
+3×
=
.
|
∴p=q=
| 1 |
| 2 |
(Ⅱ)设甲队获胜场数为ξ,则ξ的可取的值为0,1,2,3
P(ξ=0)=(
| 1 |
| 2 |
| 1 |
| 8 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 16 |
P(ξ=2)=
| C | 2 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 9 |
| 40 |
| 1 |
| 2 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 2 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
| 37 |
| 80 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 8 |
| 3 |
| 16 |
| 9 |
| 40 |
| 37 |
| 80 |
| 81 |
| 40 |
点评:本题考查概率知识的运用,考查离散型随机变量的分布列与数学期望,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
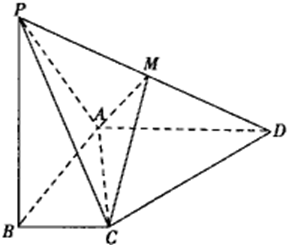 (2012•许昌一模)已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CBA=90°,面 PAB⊥面ABCD,PA=PB=AB=AD=2,BC=1.
(2012•许昌一模)已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CBA=90°,面 PAB⊥面ABCD,PA=PB=AB=AD=2,BC=1.