题目内容
(2012•许昌一模)设x,y满足
时,则z=x+y既有最大值也有最小值,则实数a的取值范围是( )
|
分析:画出约束条件表示的可行域,利用z=x+y既有最大值也有最小值,利用直线的斜率求出a的范围.
解答: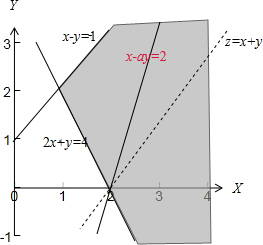 解:满足
解:满足
的平面区域如下图所示:
而x-ay≤2表示直线x-ay=2左侧的平面区域
∵直线x-ay=2恒过(2,0)点,
当a=0时,可行域是三角形,z=x+y既有最大值也有最小值,
满足题意;
当直线x-ay=2的斜率
满足:
>1或
<-2,即-
<a<0或0<a<1时,可行域是封闭的,z=x+y既有最大值也有最小值,
综上所述实数a的取值范围是:-
<a<1.
故选B.
 解:满足
解:满足
|
而x-ay≤2表示直线x-ay=2左侧的平面区域
∵直线x-ay=2恒过(2,0)点,
当a=0时,可行域是三角形,z=x+y既有最大值也有最小值,
满足题意;
当直线x-ay=2的斜率
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
综上所述实数a的取值范围是:-
| 1 |
| 2 |
故选B.
点评:本题简单线性规划的应用,直线的斜率,目标函数的最值的求法是解题的关键,考查数形结合与计算能力.

练习册系列答案
相关题目
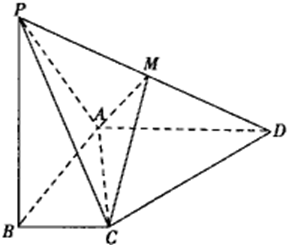 (2012•许昌一模)已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CBA=90°,面 PAB⊥面ABCD,PA=PB=AB=AD=2,BC=1.
(2012•许昌一模)已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CBA=90°,面 PAB⊥面ABCD,PA=PB=AB=AD=2,BC=1.