题目内容
（2012•许昌一模）已知（1-2x）8=a0+a1x+a2x2+…a8x8，则a1+2a2+3a3+…8a8=（ ）
分析：利用导数法与赋值法可求得a1+2a2+3a3+…8a8的值．
解答：解：∵（1-2x）8=a0+a1x+a2x2+…+a8x8，
∴两端求导得：
8（1-2x）7×（-2）=a1+2a2x+3a3x2+…+8a8x7，
令x=1得：a1+2a2+3a3+…8a8=8×（-1）×（-2）=16．
故选D．
∴两端求导得：
8（1-2x）7×（-2）=a1+2a2x+3a3x2+…+8a8x7，
令x=1得：a1+2a2+3a3+…8a8=8×（-1）×（-2）=16．
故选D．
点评：本题考查导数与二项式定理的应用，对（1-2x）8=a0+a1x+a2x2+…+a8x8两端求导是关键，也是难点，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
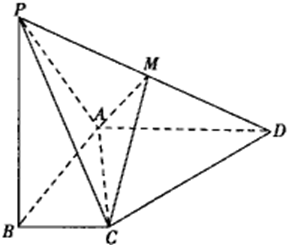（2012•许昌一模）已知四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD=∠CBA=90°，面 PAB⊥面ABCD，PA=PB=AB=AD=2，BC=1．