题目内容
若函数f(x)=
满足不等式f(1+x2)>f(ax)对任意的x恒成立,则a的取值范围是
|
-2<a<2
-2<a<2
.分析:根据分段函数的图象可以判断出函数f(x)在R上是单调递增函数,利用f(x)的单调性,将“f”去掉,从而得到关于x的不等式恒成立,求解即可得到a的取值范围.
解答:解:∵f(x)=
,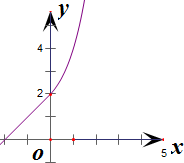
画出函数图象如右图所示,根据函数图象可以得到,函数f(x)在R上是单调递增函数,
∵(1+x2)>f(ax)对任意的x恒成立,
∴1+x2>ax对任意的x恒成立,即x2-ax+1>0对任意的x恒成立,
∴△=(-a)2-4<0,解得,-2<a<2,
∴a的取值范围是-2<a<2.
故答案为:-2<a<2.
|

画出函数图象如右图所示,根据函数图象可以得到,函数f(x)在R上是单调递增函数,
∵(1+x2)>f(ax)对任意的x恒成立,
∴1+x2>ax对任意的x恒成立,即x2-ax+1>0对任意的x恒成立,
∴△=(-a)2-4<0,解得,-2<a<2,
∴a的取值范围是-2<a<2.
故答案为:-2<a<2.
点评:本题考查了分段函数的单调性,以及利用函数的单调性解不等式.对于分段函数的问题,一般选用数形结合的数学思想方法或运用分类讨论的数学思想方法.属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
若函数f(x)=
,则f(x)的最大值为( )
|
| A、9 | B、8 | C、7 | D、6 |