题目内容
已知椭圆E的中心在坐标原点、对称轴为坐标轴,且抛物线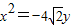 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点 在该椭圆上.
在该椭圆上.(1)求椭圆E的方程;
(2)若斜率为
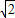 直线l与椭圆E交于不同的两点B、C,当△ABC面积的最大值时,求直线l的方程.
直线l与椭圆E交于不同的两点B、C,当△ABC面积的最大值时,求直线l的方程.
【答案】分析:(1)求出抛物线的焦点,即得椭圆的焦点,设出椭圆方程为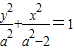 将点A(1,
将点A(1,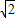 )代入,求出a,即得椭圆方程;
)代入,求出a,即得椭圆方程;
(2)用待定系数法设直线BC的方程为y=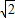 x+m,将其与椭圆的方程联立求同弦长BC,再求出点A到此弦的距离,将三角形的面积用参数表示出,判断出它取到最大值时的参数m的值即可得到直线l的方程
x+m,将其与椭圆的方程联立求同弦长BC,再求出点A到此弦的距离,将三角形的面积用参数表示出,判断出它取到最大值时的参数m的值即可得到直线l的方程
解答:解:(1)由已知抛物线的焦点为(0,-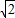 ),故设椭圆方程为
),故设椭圆方程为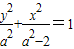 .
.
将点A(1,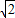 ),代入方程得
),代入方程得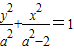 ,,得a2=4或a2=1(舍)(4分)
,,得a2=4或a2=1(舍)(4分)
故所求椭圆方程为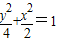 (5分)
(5分)
(2)设直线BC的方程为y=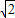 x+m,设B(x1,y1),C(x2,y2)
x+m,设B(x1,y1),C(x2,y2)
代入椭圆方程并化简得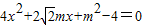 ,
,
由△=8m2-16(m2-4)=8(8-m2)>0可得m2<8,①
由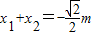 ,
,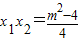
故|BC|=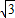 |x1-x2|=
|x1-x2|=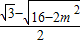 .
.
又点A到BC的距离为d=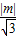
故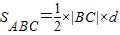 =
=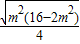 ≤
≤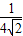 ×
×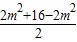 =
=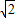
当且仅当2m2=16-2m2,即m=±2时取等号(满足①式),S取得最大值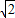 .
.
此时求直线l的方程为y=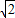 x±2.
x±2.
点评:本题考查直线与圆锥曲线的综合问题,解题的关键是设出直线的方程,根据直线与圆锥曲线的位置关系,将三角形的面积用参数表示出来,本题解题过程中利用判别式判断出最值取到时参数的值,这是本题中的一个难点,由于对知识掌握得不熟练,答题者可能到这里就不知道怎么来求参数的值,导致解题失败,数学学习,知识掌握得全面是灵活运用的基础.
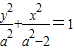 将点A(1,
将点A(1,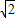 )代入,求出a,即得椭圆方程;
)代入,求出a,即得椭圆方程;(2)用待定系数法设直线BC的方程为y=
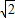 x+m,将其与椭圆的方程联立求同弦长BC,再求出点A到此弦的距离,将三角形的面积用参数表示出,判断出它取到最大值时的参数m的值即可得到直线l的方程
x+m,将其与椭圆的方程联立求同弦长BC,再求出点A到此弦的距离,将三角形的面积用参数表示出,判断出它取到最大值时的参数m的值即可得到直线l的方程解答:解:(1)由已知抛物线的焦点为(0,-
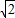 ),故设椭圆方程为
),故设椭圆方程为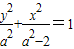 .
.将点A(1,
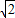 ),代入方程得
),代入方程得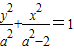 ,,得a2=4或a2=1(舍)(4分)
,,得a2=4或a2=1(舍)(4分)故所求椭圆方程为
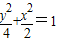 (5分)
(5分)(2)设直线BC的方程为y=
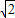 x+m,设B(x1,y1),C(x2,y2)
x+m,设B(x1,y1),C(x2,y2)代入椭圆方程并化简得
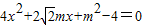 ,
,由△=8m2-16(m2-4)=8(8-m2)>0可得m2<8,①
由
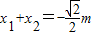 ,
,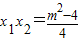
故|BC|=
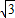 |x1-x2|=
|x1-x2|=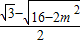 .
.又点A到BC的距离为d=
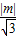
故
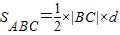 =
=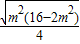 ≤
≤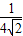 ×
×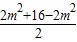 =
=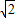
当且仅当2m2=16-2m2,即m=±2时取等号(满足①式),S取得最大值
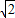 .
.此时求直线l的方程为y=
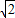 x±2.
x±2.点评:本题考查直线与圆锥曲线的综合问题,解题的关键是设出直线的方程,根据直线与圆锥曲线的位置关系,将三角形的面积用参数表示出来,本题解题过程中利用判别式判断出最值取到时参数的值,这是本题中的一个难点,由于对知识掌握得不熟练,答题者可能到这里就不知道怎么来求参数的值,导致解题失败,数学学习,知识掌握得全面是灵活运用的基础.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目